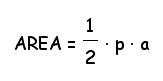|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Content Objective:
Students will deduce the general expressions for perimeter and area of an n-sided polygon based on the previous lessons.
Students will understand the concept of representing the number of sides of a regular polygon with the variable n.
Procedure:
1. Collectively recall the various expressions discovered from the previous lessons. As a class, ask students to complete the following chart. Again, all of the side lengths of our shapes are of length s.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. To generalize our perimeter expressions, ask students the following questions:
What do you expect the perimeter to be for a 12-sided regular polygon? What about a 20-sided polygon?
Can you make a generalization for polygons who have n number of sides?
Finally, what is the general expression for the perimeter of regular polygons, in terms of the side length of s and having n number of sides?
1. Collectively recall the various expressions discovered from the previous lessons. As a class, ask students to complete the following chart. Recall method 1 for finding area was the sum of smaller shapes inside the polygon. Method 2 resulted from a general formula introducing the apothem.
SHAPE PRIOR KNOWLEDGE METHOD 1 METHOD 2 Triangle Square Pentagon Hexagon 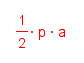
Octagon
2. Discuss the area chart above, and ask students the following questions:
Why is method 1 for the regular octagon so different from method 1 for regular pentagon and regular hexagon?
We can see the general expressions for area in method 2 are the same. What variables do these expressions depend on?
Make a conjecture about the area of a 10-sided regular polygon. What about a 12-sided regular polygon? What values would you have to find in order to compute area?
Can you make a generalization for polygons who have n number of sides?
Finally, what is the general expression for the area of regular polygons, in terms of the side length of s and having n number of sides?
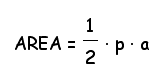
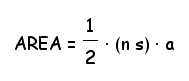
For ALL regular polygons?
It is useful to help students understand this expression for ALL regular polygons, even ones for which we already know their area formulas. Since this is a general formula for any n-sided regular polygon, we would expect it to also apply to regular triangles (i.e. a 3-sided regular polygon).
So, ask students if this is true? How can we show that this general expression is the same as the area expression for triangles on the chart above?
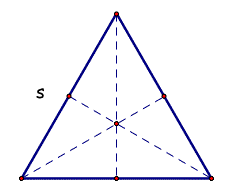
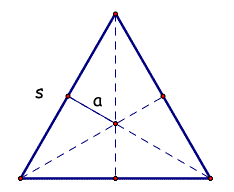
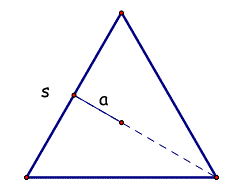
Given that the apothem length is 1/3 the length of the height, let's evaluate our expression to see if we can arrive at the same area formula we already knew.
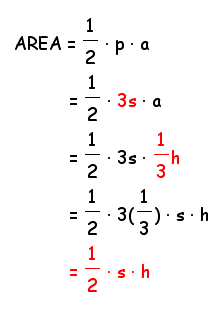
Therefore, this general expression for area does work for regular triangles!
Click here to view
the GSP sketch of the regular triangle.
We expect this general formula to also hold true for squares. Let's find out!
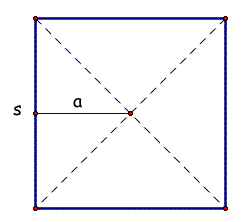
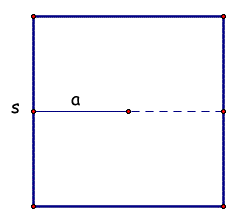
We can see here that the apothem length is 1/2 the length of the side. Now, let's evaluate our expression to see if we can arrive at the same area formula we already knew.
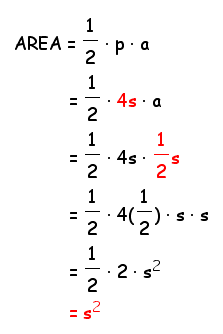
Therefore, this general expression for area does work for squares!
Click here to view
the GSP sketch of the square.