

Content Objective:
Students will learn the method of finding the perimeter of regular octagons, similar to the previous lessons.
Students will use the methods discussed with regular hexagons to find the area of regular octagons. (The use of two different methods to find the area will help students understand the concept of using multiple problem solving techniques to produce the same result.)
Materials:
Rulers for pairs, octagon perimeter worksheet, octagon area worksheet
Procedure:
1. Collectively recall the definition of perimeter given on review day. Have students get into pairs and distribute the octagon perimeter worksheet. Once worksheet is complete and students have compared their answers, ask the class as a whole the following questions:
What do you notice about the side lengths of our octagon? Is this what you expected?
What happens to the perimeter when the side lengths are changed?
Is there a way to find the perimeter of a regular octagon without measuring all eight sides?
Recalling the general expressions for the perimeter of regular hexagon? Do you notice a pattern? What can we expect when we discover the perimeter of a regular octagon?
2. Demonstrate using Geometer's Sketchpad the properties of the side lengths of regular octagon. Click here to use the GSP file and watch the animation for the changing perimeter.

Similar to the hexagon and pentagon, first we will divide the regular octagon into parts to find the area. Then, we will identify and use the apothem to find the area of our regular octagon and compare both of the methods.
METHOD 1:
Begin by showing the figures below and ask the following questions:
Click here to view the GSP sketch of these images.



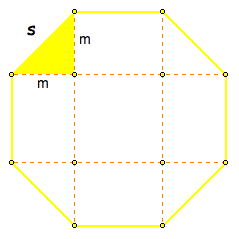
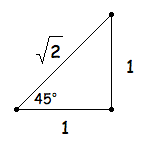

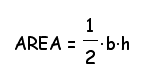
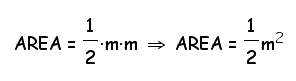

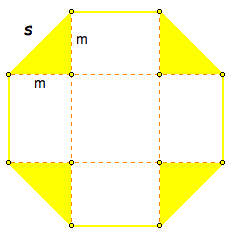


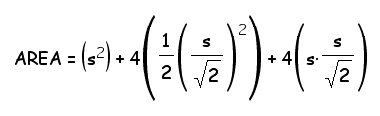
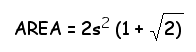
If necessary, review the algebra steps involved in the simplification process with students. Click to view the algebra steps. Click here for the Geometer's Sketchpad file for the regular octagons.
So we have discovered a general formula for the area, using the smaller shapes inside the octagon!
Example 1:
Use the above area expression to calculate the area of an octagon with side length of s = 3.00 cm for comparison with method 2 later. Ask the students to identify the values of m and s in this example, before computing the area.
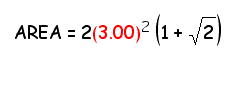
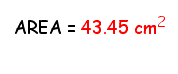
METHOD 2:
And now, using the apothem we can find the area in fewer steps. First, let's revisit the octagon that was broken into triangles.
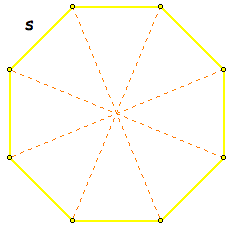


Example 2:
Now, we can fill in the values for s and a to find the area of this regular octagon. Again, let s = 3.00 cm and let a = 3.62 cm. What is the area?

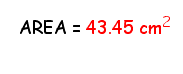
COMPARING METHODS:
Discuss with students the two different methods for finding the area of a regular octagon.
As a class, discuss the advantages and disadvantages for each of the methods and ask the following questions:
Which method is easier to formulate?
Which method produces quicker results?
Will these methods ever produce different answers?
Finally, distribute the octagon area worksheet and have students complete in groups, using either method. Then, as a class, compare answers and discuss the methods for finding the solutions.
Demonstrate using Geometer's Sketchpad the
properties of the side lengths and apothem lengths of regular
octagons. Click here to use the
GSP file and watch the animation for the changing area.
Return to Instructional Unit