

This is an equation of a parametric curve.
Definition: Parametric Curve
A parametric curve C in the plane is a pair of functions x=f(t), y=g(t), that give x and y as continuous functions of the real number t (the parameter) in some interval I. Every value of the parameter t determines a point (f(t),g(t)) and the set of all such points is the graph of the curve C. The two equations are called the parametric equations of the curve.
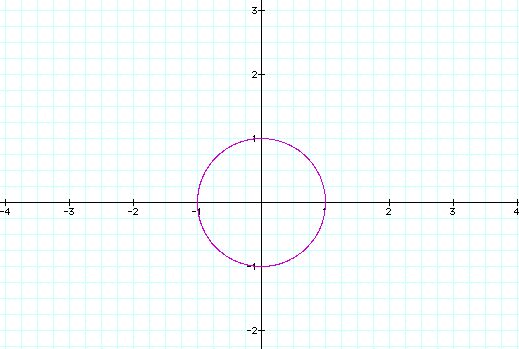
The graph of this curve is the unit circle when the values of a and b are both 1. To verify this, we note that the fundamental identity of trigonometry gives x^2+y^2 = cos^2t=sin^t = 1. This implies that every point of the graph lies on the circle with equation x^2+y^2=1.
Next we investigate the curve for various values of a and b. In the next graph, a is increased to 2 while be is held constant. The shape of the graph of this curve is shown below. It still ranges from -1 to 1 on both the x and y-axis, but the shape has changed drastically.
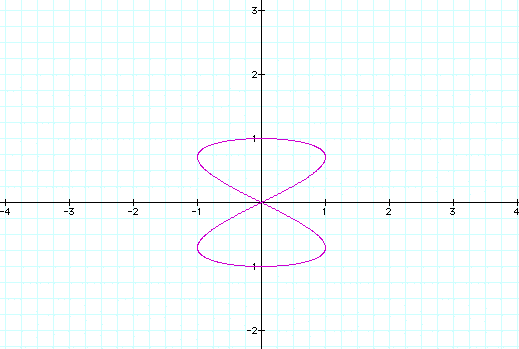
Increasing a to 2 caused the graph to form two loops (an hour-glass shape) symmetrical about the x and y-axis.
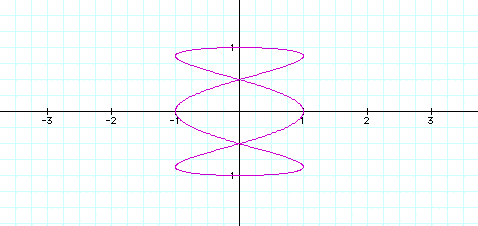
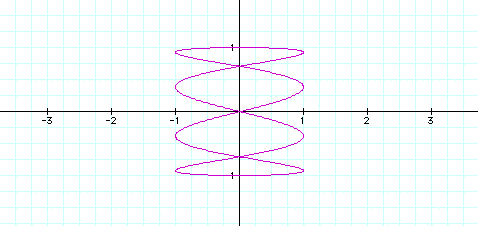
As can be seen from the four graphs above, increasing a from 1 to 2 to 3,.. to 5 caused the number of loops in the graph to increase respectively.
Next we look at changes in b.
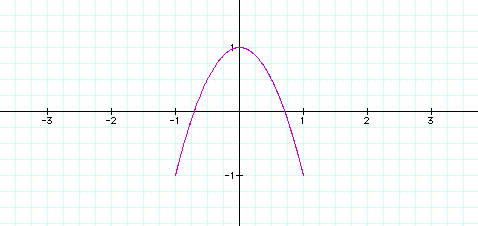
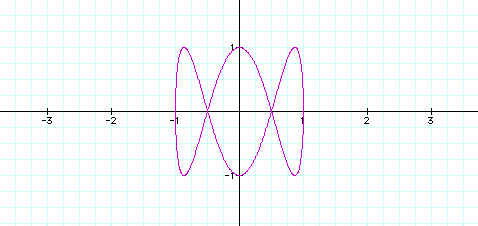
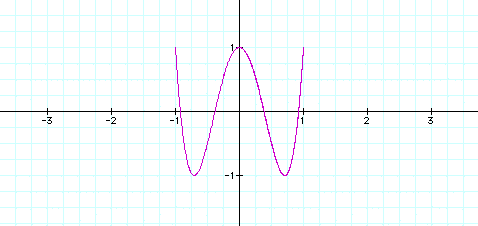
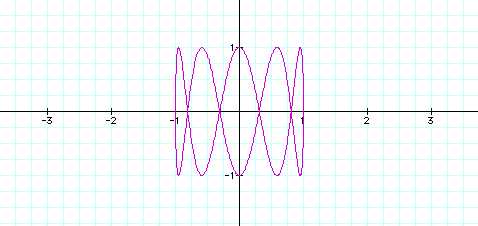
Increases in the value of b cause the graph to alternate between a function when b is an odd integer and a relation with loops (as with changes in a) when b is an even integer. However in this case the graph is rotated 90 degrees.
In concluding this investigation we note that the use of parametric equations x=x(t), y=y(t) is most advantageous when elimination of the parameter is either impossible or would lead to an equation y=f(x) that is much more complicated than the original parametric equation. We also note that a curve given in polar coordinates by the equation r=f(theta) can be regarded as a parametric curve with parameter theta.