

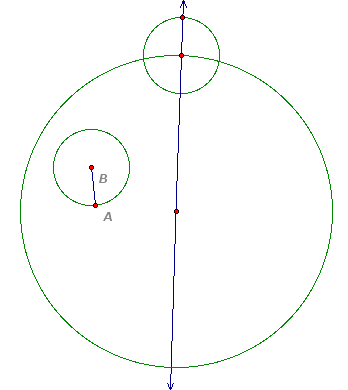
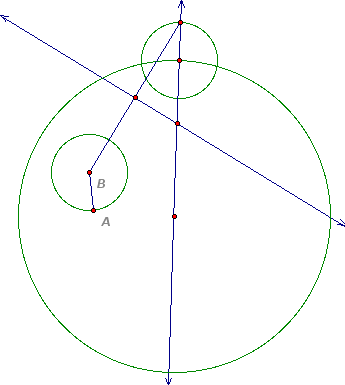
This investigation begins with the following problem. How do we construct the configuration below and determine the locus of the centers of all such circles tangent to the two given circles?
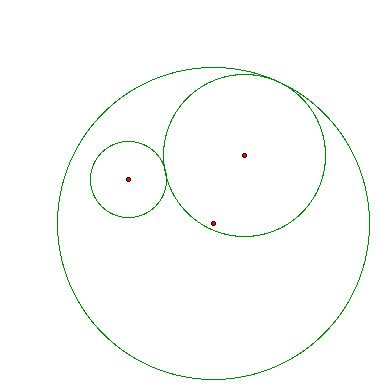
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
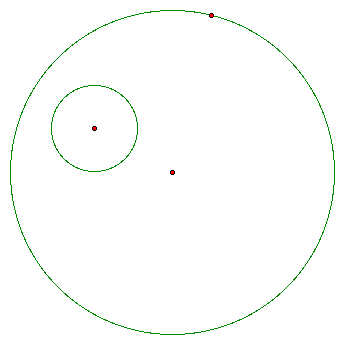
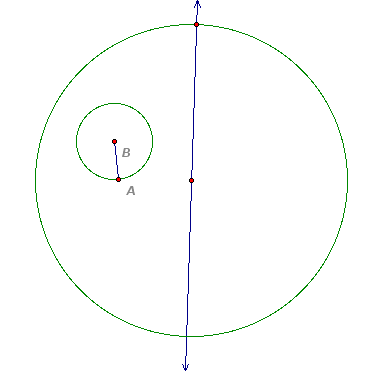
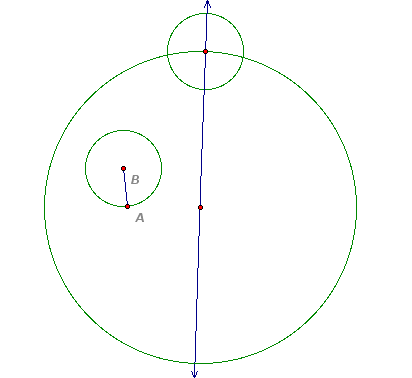
The circle centered on the larger circle has radius AB.
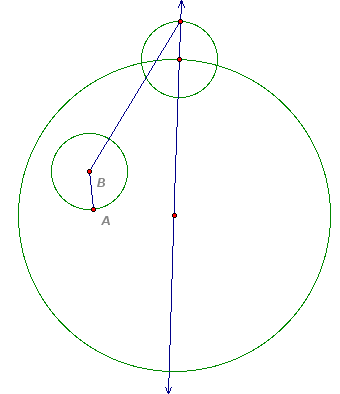
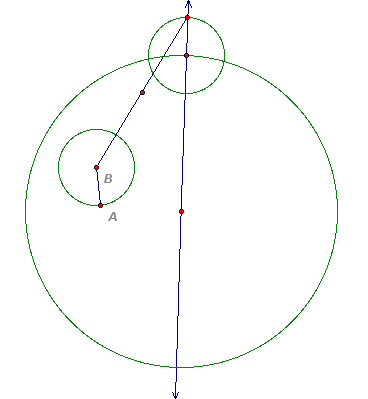
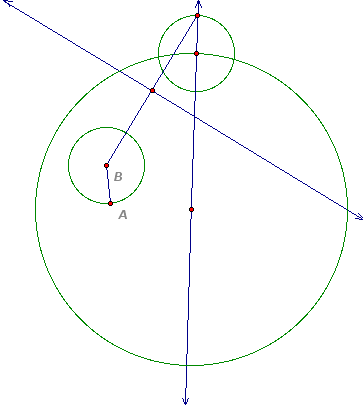
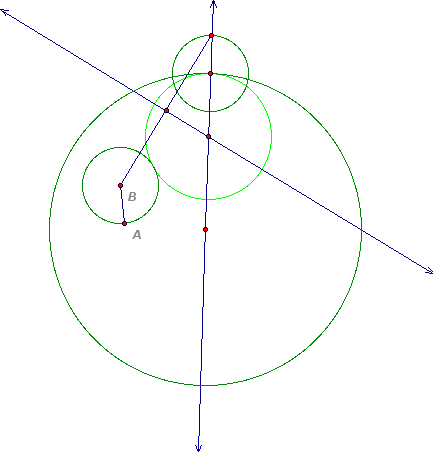
The last line added is the perpendicular bisector of the segment. The intersection of the two lines is the center of the tangent circle.
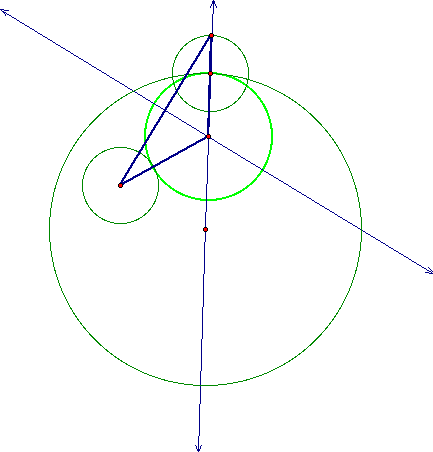
Notice the isosceles triangle connecting the centers of the circles in this completed construction.
With GSP, we can animate around the circle and trace the locus of all circles tangent to the two circles.
When we trace the center of the tangent circle, it forms an ellipse.
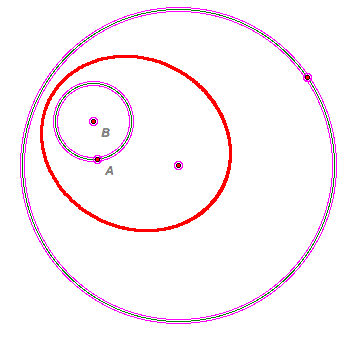
Click here then when the GSP file appears, click the animation bottom to see the trace of the the locus of centers of all circles tangent to the given two circles.