

In this assignment The graph of the equation
is considered for different values of a, b, or c as the other two are held constant.
When a is 1 and b and c are both 0 we get the following graph of the parabola.

Here the vertex of the parabola, "the point at which it changes direction", is at the origin.
In the next three graphs we let c vary while a and b are held constant at 1.



In the three graphs above, a and b are held constant while c is varied. As c varies, the graph is shifted along the y axis.
Next are a few graphs where a varies and b and c are held constant.



From the graphs above we can see that as a varies while b and c are held constant the, "size" of the coefficient a determines the "width" of the parabola. the sign of a determines the direction in which the parabola opens. If a > 0 the curve opens upwards. If a < 0 the curve opens downwards. Specifically, the larger a > 0 is the steeper the curve rises, therefore the narrower the parabola.
Next we vary b while a and c are held constant at 1.






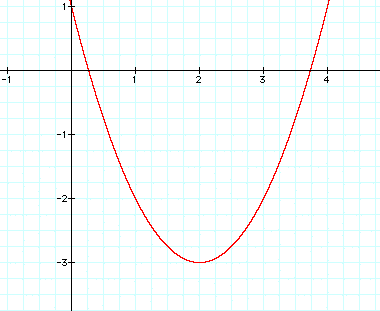
From the graphs 6 graphs above we can see what happens when b varies as a and c are held constant (a = 1, c = 1). All of the graphs pass through the point y = 1.

In this family of graphs, a and c are held constant while b varies over the integers -3 to +3. All of the graphs intersect at a common point on the y axis.
Click here to see animation.
Next lets consider the question of whether the locus of the vertices of a set of parabolas is a parabola. Consider the graph below. In it we we let b vary from -3 to 3 while a and c are held constant at 1. We then interpose the graph of y=-x^2+1.


From this graph it appears that the vertex of each of the graphs is a solution of the equation y=-x+1. In fact, calculations (beyond the scope of this investigation) do show this to be true.
Next we graph the equation in the xb-plane. The graph of the equation is a hyperbola. Notice the graph when b=2 and b=-2 we get roots at the vertex of the hyperbola. When b> 2, or b<- 2 the equation has 2 real roots. However, when-2< b < 2 there are no real roots.
Now lets look at what happens when c = -1 and c =1.

When we let c =-1 the graph approaches a diagonal asymptote and the vertical axis.