

This assignment is to construct four centers of a triangle, the Centroid (G), the Orthocenter (H), the Circumcenter (C) and the Incenter (I). Also, the Centroid is explored for different shapes of triangles.
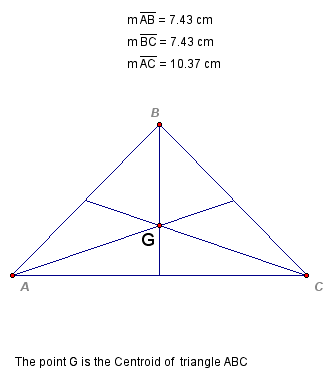
The Centroid of a triangle is the common intersection of the three medians. A median of a triangle is the line segment from a vertex to the midpoint of the opposite side.
Here we have an acute triangle with the Centroid displayed as the intersection of the three line segments drawn from each vertex to the midpoint of the opposite side.
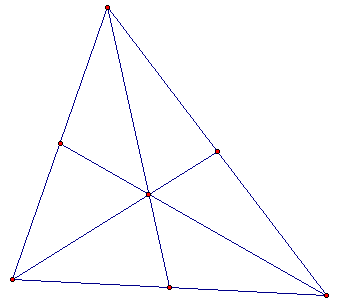
This is an equilateral triangle.
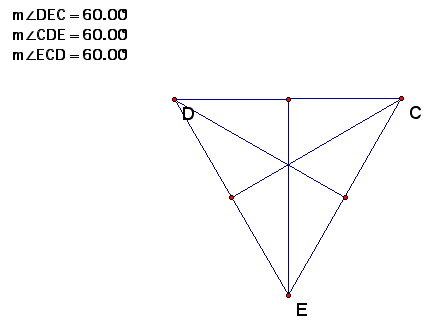
In this equilateral triangle (any equilateral triangle) the Centroid and Orthocenter are the same.
Next we have a right triangle. In this triangle, the Centroid is at angle c, the right angle.
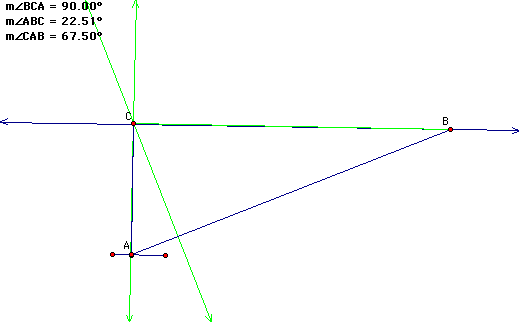
This is an isoceles triangle
Click here to see the GSP sketch
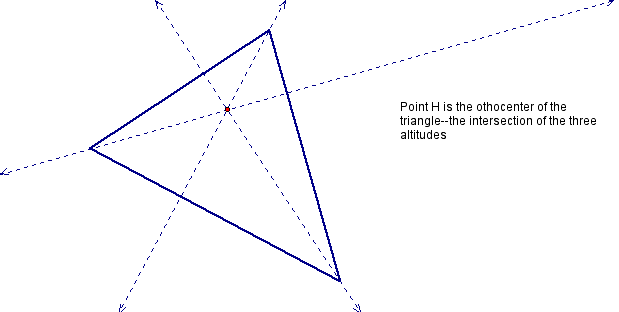
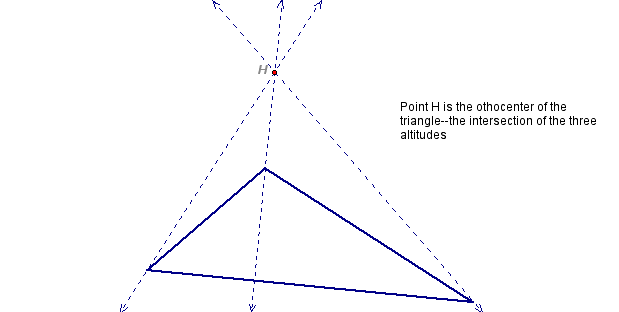
Click here to see the GSP sketch
For any acute triangle the point of concurrence of the medians is called the Centroid of the triangle. It is the center of gravity of a triangular equal density object.
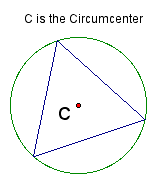
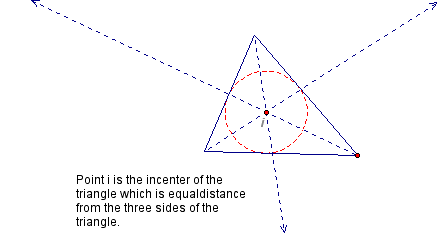
Click here to see the GSP sketch
In the next triangle the Orthocenter, Centroid, Circumcenter and Incenter are displayed.
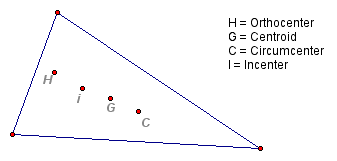
Click here to see the GSP sketch
In an equilateral triangle the Orthocenter, Centroid, Circumcenter and Incenter are the same.
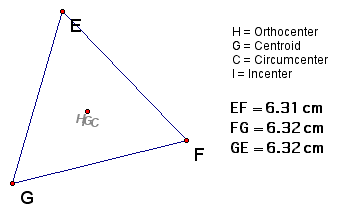
In this assignment, (assignment 4) the centers of triangles were explored.