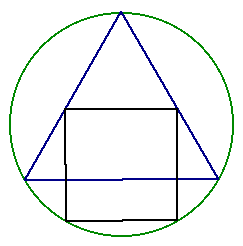
Constructing the inscribed figure can also be accomplished through a sort of connect-the-dots method.

As we have seen, the vertices of the equilateral triangle and two vertices of the square lie on points contained in the set of 12 equally spaced points on a circle.
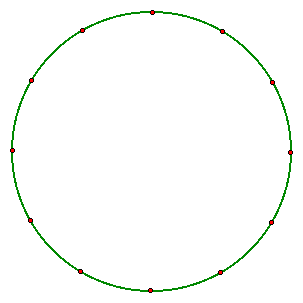
Using these points and a straightedge, one can quickly construct the original equilateral triangle.
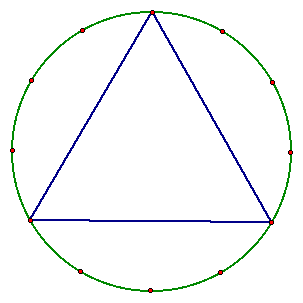
Additionally, the side of the square can be constructed by connecting the points on either side of one particular point. For convenience, we have chosen to connect the following two points.
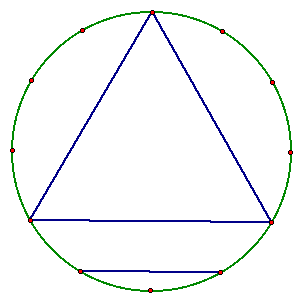
Finding the intersection of perpendicular lines through these two points with the sides of the triangle are all that remain for this construction.
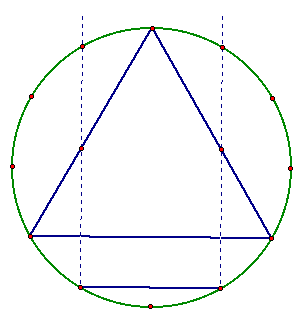

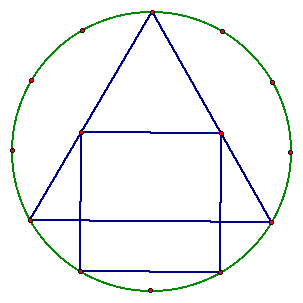
And so we have another method of constructing the figure.