
Using a bit of trigonometry, we discovered the following algebraic representation and Cartesian graph of the quadratrix.

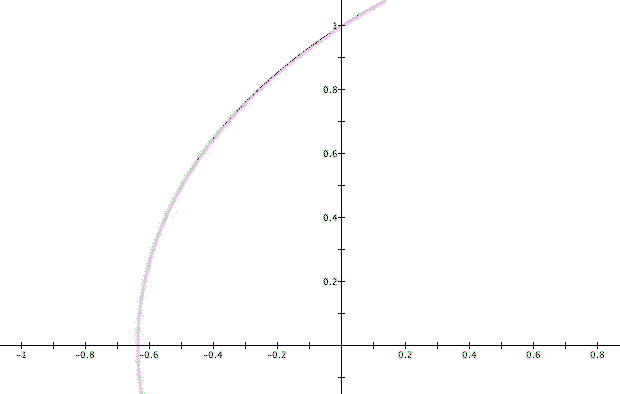
While locating the y-intercept was a trivial matter, the location of the x-intercept looks more challenging. Let's take a look.
A first method of finding an x-intercept is substituting 0 for the y-value of the equation. Take a look at what happens when we try this . . .
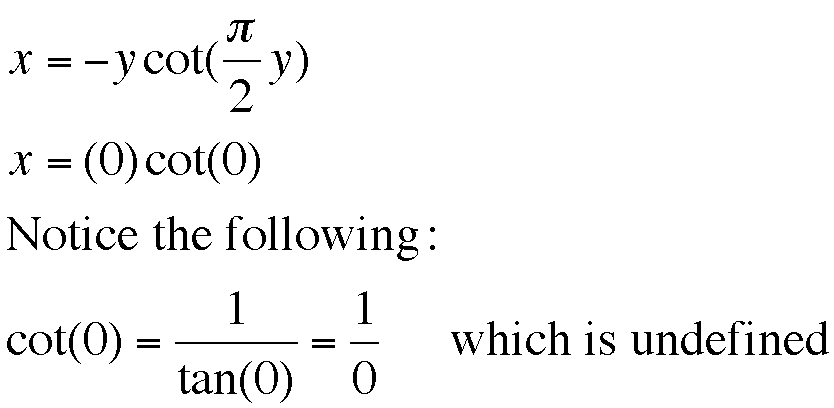
Thus making sense of x=(0)cot(0) becomes tricky.
To help us with this problem, we can incorporating limits. In particular, it makes sense to take a look at the limit of our equation as y approaches 0.
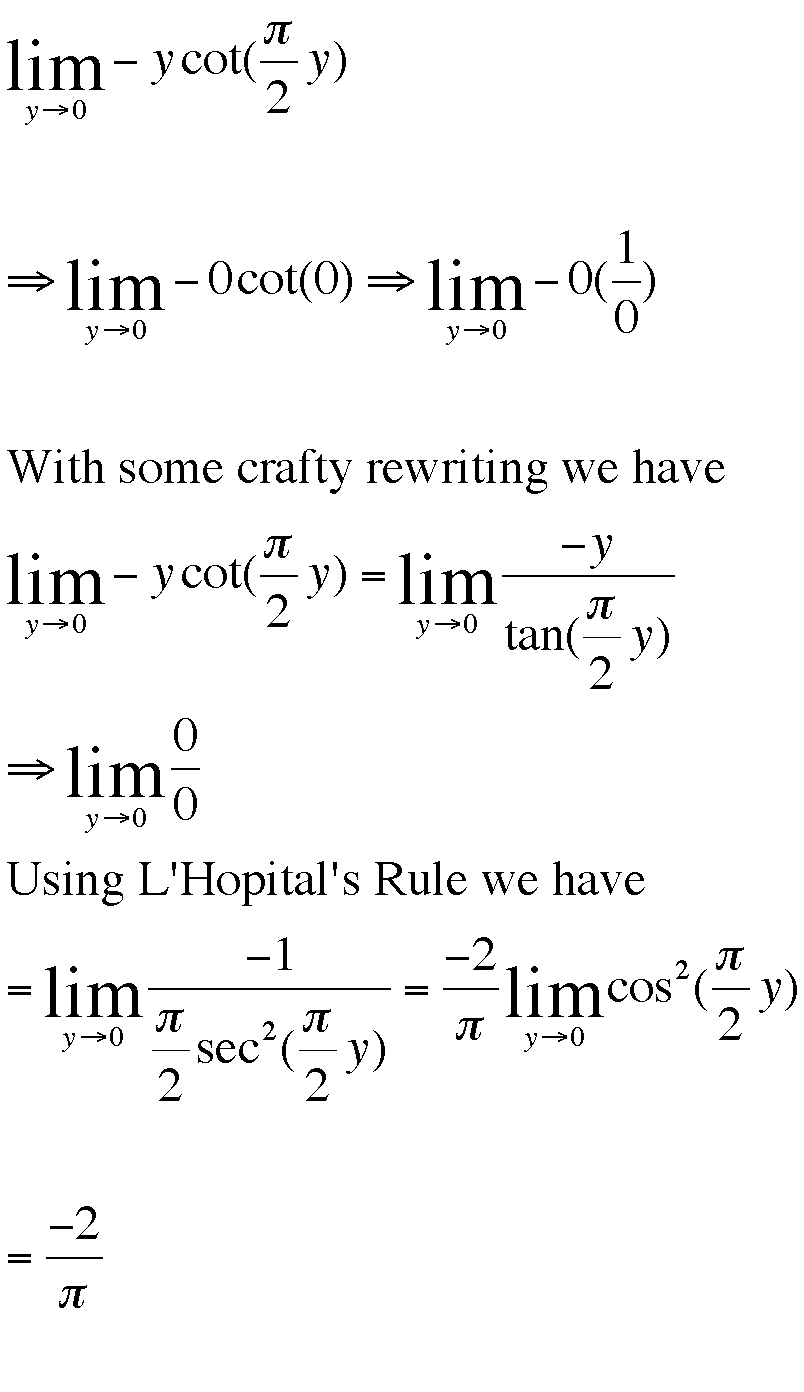
Ah hah! It appears that as y approaches 0, x approaches -2/pi. We find that the graph of our equation does not, in fact have an x-intercept because their is a hole at that point. However, in trying to understand the geometry of our quadratrix, we discover that the segment between the center of the circle and the termination point of the quadratrix curve can be thought of as having length 2/pi.
An application of this x-intercept is used
in the Squaring the Circle problem. Check it out here.
Back to