Assignment 1
The purpose of this activity is to explore binary operations of functions and the composition of functions.
Start
with two linear functions: f(x) and g(x).
Let
f(x) = x/5 - 4
g(x) = -3x + 2
f(x) is the function shown in purple and g(x) is the function shown in red. The slope of f(x) is 1/5 and the intercept is -4. The slope of g(x) is -3 and the intercept is 2. We can verify this information by looking at the graphs of these equations show below.
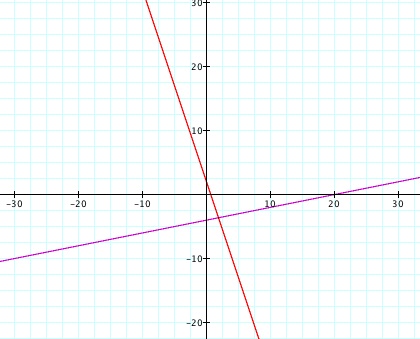
Let
f(x) = x/5 - 4
g(x) = -3x + 2
f(x) is the function shown in purple and g(x) is the function shown in red. The slope of f(x) is 1/5 and the intercept is -4. The slope of g(x) is -3 and the intercept is 2. We can verify this information by looking at the graphs of these equations show below.

Now explore the graph of h(x), where h(x) = f(x) +
g(x). Notice how this graph relates to the original
functions.
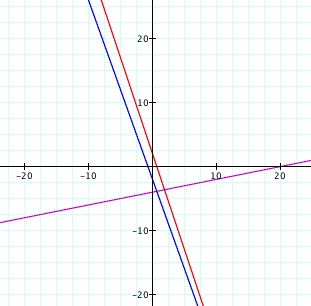
Notice the slope of this new function appears to be very similar to that of g(x). Algebraically, this function can be shown as h(x) = -(14/5)x -2. The slope is -14/5 and the y - intercept is -2.
Let's now explore the graph of h'(x), where h'(x) = f(x).g(x).
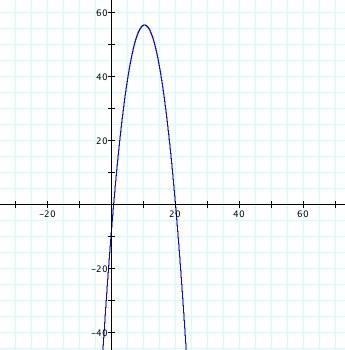
Here we can see that the graph of two linear functions multiplied together is in this case a parabola.
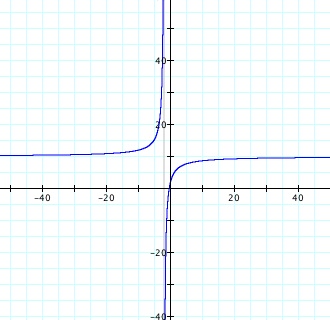
Let's now explore the graph of h''(x) where h''(x) = f(x)/g(x).
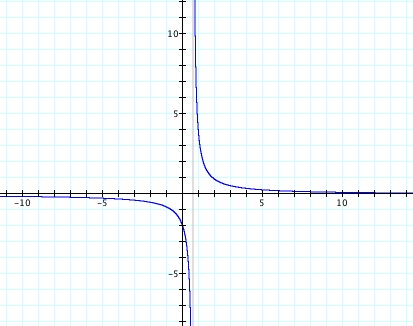
Here we notice that the graph is a hyperbola.
Lastly, look at the graph of h'''(x), where h'''(x) = f(g(x)).
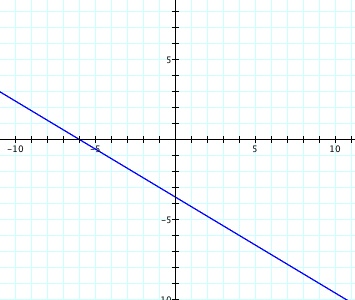
The compositions of these two functions, f of g of x, is a linear function.
Now, let f(x) and g(x) be two different functions and explore these graphs again.
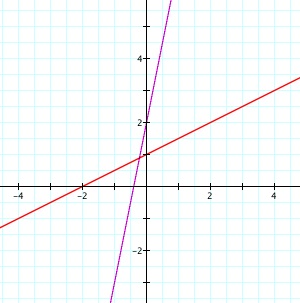
Let f(x) = 5x + 2, and let g(x) = x/2 + 1.
Below are the graphs of these two equations. f(x) is the purple graph and g(x) is the red graph.
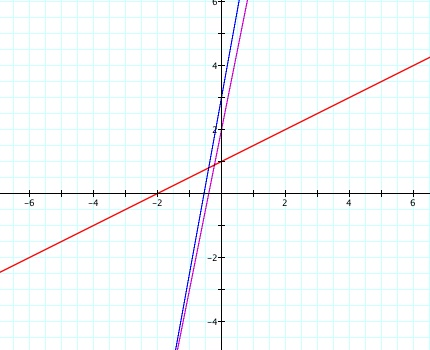
h(x) = f(x) + g(x) is shown by the blue function. Again, notice how the process of addition causes the original equation with the largest absolute value to dominate.
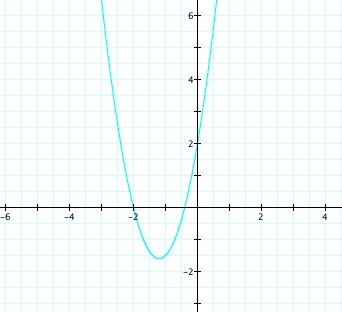
h'(x) = f(x).g(x) Again, when we multiply two linear equations together, we get a parabola.
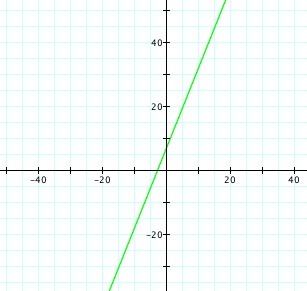
h'''(x) = f(g(x)) The composition of two linear functions, f of g of x, creates a new function, also linear.
Summary of Findings
When two linear functions are added together, the result is a third linear function. The slopes and y-intercepts of the functions follow the basic properties of addition when added together, respectively.
When two linear functions are multiplied together, the resulting function will be a parabola, provided that the slope of neither function is 0. In that case, the resulting function will either be a linear function (if one function has zero slope) or a constant function (if both functions have zero slopes.) Likewise, the resulting function when one linear function is divided by another will be a hyperbola, provided neither function has a zero slope. If a linear function with a non zero slope is divided by a function with a zero slope, the resulting function will also be linear.
The composition of two linear functions always yields another linear function.
Return to my homepage

Notice the slope of this new function appears to be very similar to that of g(x). Algebraically, this function can be shown as h(x) = -(14/5)x -2. The slope is -14/5 and the y - intercept is -2.
Let's now explore the graph of h'(x), where h'(x) = f(x).g(x).

Here we can see that the graph of two linear functions multiplied together is in this case a parabola.
Let's now explore the graph of h''(x) where h''(x) = f(x)/g(x).

Here we notice that the graph is a hyperbola.
Lastly, look at the graph of h'''(x), where h'''(x) = f(g(x)).

The compositions of these two functions, f of g of x, is a linear function.
Now, let f(x) and g(x) be two different functions and explore these graphs again.
Let f(x) = 5x + 2, and let g(x) = x/2 + 1.
Below are the graphs of these two equations. f(x) is the purple graph and g(x) is the red graph.

h(x) = f(x) + g(x) is shown by the blue function. Again, notice how the process of addition causes the original equation with the largest absolute value to dominate.

h'(x) = f(x).g(x) Again, when we multiply two linear equations together, we get a parabola.

h''(x) = f(x)/g(x) Dividing one linear equation
by another yields a hyperbola.

h'''(x) = f(g(x)) The composition of two linear functions, f of g of x, creates a new function, also linear.

Summary of Findings
When two linear functions are added together, the result is a third linear function. The slopes and y-intercepts of the functions follow the basic properties of addition when added together, respectively.
When two linear functions are multiplied together, the resulting function will be a parabola, provided that the slope of neither function is 0. In that case, the resulting function will either be a linear function (if one function has zero slope) or a constant function (if both functions have zero slopes.) Likewise, the resulting function when one linear function is divided by another will be a hyperbola, provided neither function has a zero slope. If a linear function with a non zero slope is divided by a function with a zero slope, the resulting function will also be linear.
The composition of two linear functions always yields another linear function.
Return to my homepage