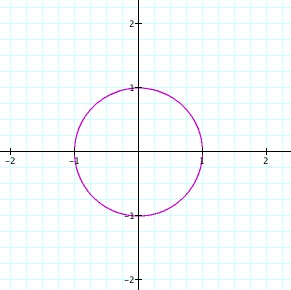
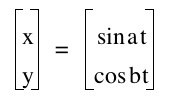When a=b, this graph will always be a circle with radius 1.
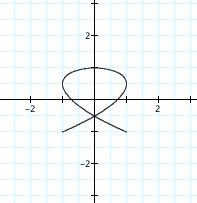
What happens when a and b are different values? For fun, let a =
3 and let b = -2.
If you would like to explore the graph of
this equation when a and b are different values, click here!
Let's now look at the graph of
x = a cos(t)
y = b sin (t)
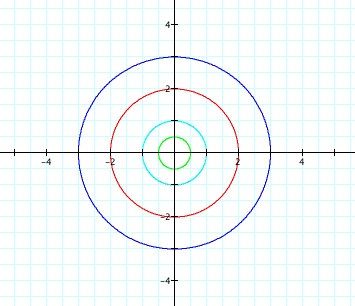
Let a=b and explore different values of a=b.
As you can see from the graph, we get a set of concentric
circles. The radius of each circle is determined by the value of
a=b.
Now let's explore what happens when a does not equal b.
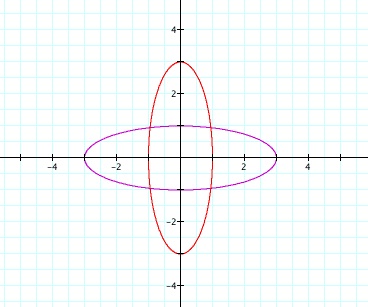
For the red ellipse below, a=3 and b=1.
For the purple ellipse below, b=1 and a=3.