Assignment
6
This activity explores
the properties of a triangle
whose sides are the medians of some original triangle
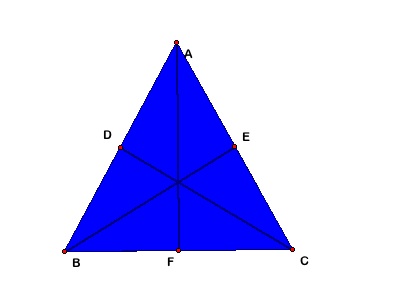
For this exploration we will construct a triangle and its medians. We
will then a second triangle with the three sides having the lengths
of the three medians from your first triangle. The focus of this
exploration is to investigate the relationship between these two
triangles.
First construct a
triangle and its medians.
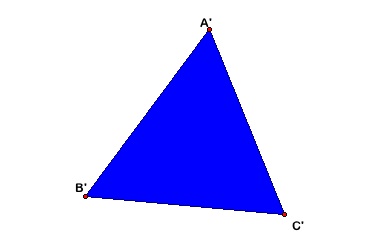
Next, construct a second triangle
with the three sides having
the lengths
of the three medians from your first triangle.
The goal of this exploration is to
find some relationship
between the two triangles.
Click here for an interactive java
sketchpad sketch of these two triangle. Use this sketch to
investigate the relationship of these two triangles. What do you
notice about the perimeters? About the areas? What about
the ratio of perimeters? The ratio of areas?
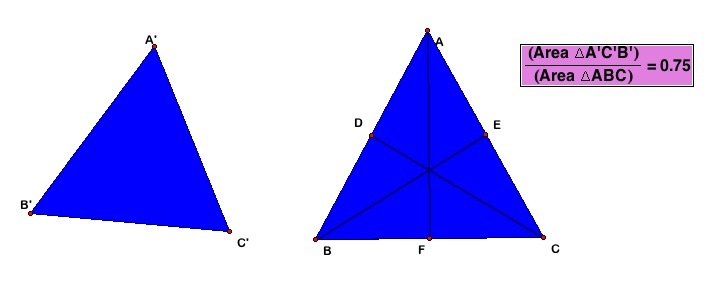
This section will investigate
the relationship shown
below. That is, that the ratio of the area of the median triangle
to the area of the original triangle is .75 or 3/4.
Another way of representing this
concept is the picture below. The proof that follow uses this
next figure as a reference.
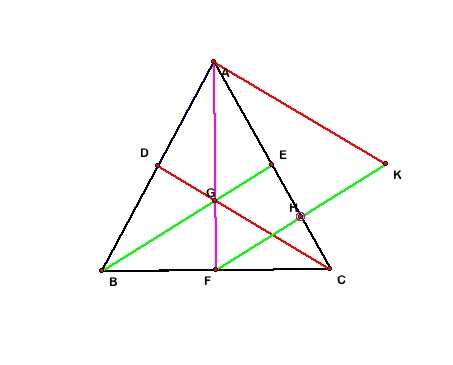
Proof:
Suppose the area of triangle ABC
is 24. (This number is chosen because it is divisible by 2, 3, 4,
and 6.) Given that BE is a median (BE divides ABC into two equal
pieces), the area of triangle ABE is 12. We know that GE =
BE/3, because G is the centroid of the triangle. Then the area of
AGE is 12/3 or 4. FK is parallel to BE, by construction, and F is
the midpoint of BC, therefore, H is the midpoint of EC. Then
AE/AH = 2/3. It follows that the area of AGE / the area of AFH =
(2/3) (2/3) or 4/9. Since the area of AGE = 4, the area of AFH =
9. Since H is the midpoint of FK, then the area of AFH is one
half the area of AFK. So the area of AFK is 18 which is 3/4 the
area we started with.
Return to my homepage