Assignment 8
Altitudes and
Orthocenters
In this activity we will investigate properties of altitudes and
orthocenters
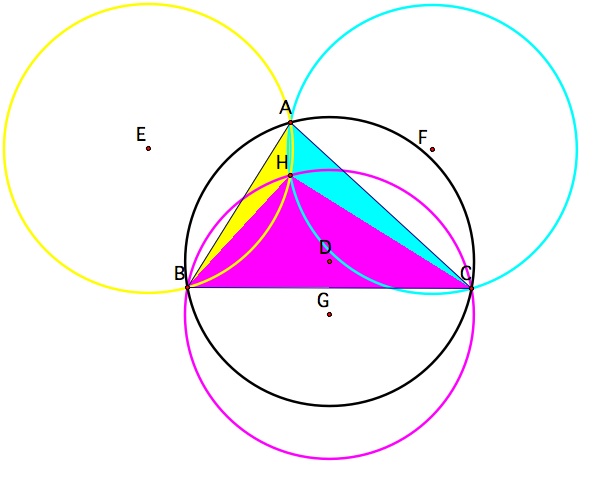
Start by constructing any triangle ABC.
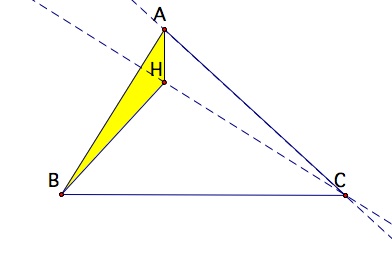
Construct the orthocenter H of triangle ABC. Remember the
orthocenter of a triangle is the point of intersection of any two
altitudes of the triangle. Notice that the orthocenter lies in
the interior of triangle ABC, since ABC is an acute triangle.
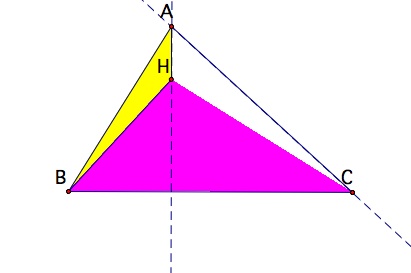
Construct
the orthocenter of triangle HAB. Remember that the orthocenter of
HAB will lie outside the triangle since HAB is obtuse. Notice that the
othocenter of HAB
coincides with point C of the original triangle.
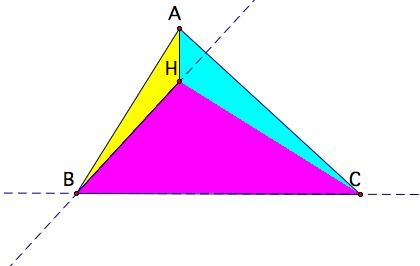
Now construct the orthocenter of triangle HBC. This time the
orthocenter lies coincident with point A. It appears that when a
triangle is constructed from two vertices and the orthocenter of an
original triangle, the orthocenter of the constructed triangle lies
coincident with the vertex of the original triangle not included in
the constructed triangle.
Let's test the above observation by constructing the orthocenter
of
triangle HAC. Again, notice that the orthocenter of triangle HAC
lies coincident with point B, the only vertex of the original triangle
not included in the constructed triangle.
Now let's investigate the circumcircles of these four
triangles.
Construct the circumcircles of triangles ABC, HBC, HAB, and
HAC.
Each of the
constructed circumcircles are congruent to one
another. Click here for an
interactive javasketchpad exploration. Drag each of the
vertices of the original triangle one at a time to coincide with
orthocenter H. Notice that each of the three circumcircles of the
smaller triangles are congruent to the circumcircle of triangle ABC.
Return to my homepage