Assignment
4
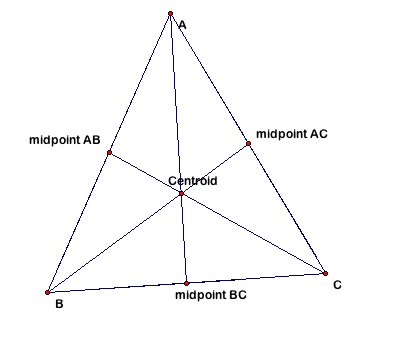
Centroid of a triangle
This activity is designed to
help students explore the properties of the centroid of a
triangle using Geometer Sketch Pad. This activity assumes
students already have basic familiarity with GSP.
The centroid of a triangle is the
common
intersection of the three medians. Follow the instructions below to
construct the centroid of a triangle.
1. Open Geometer Sketch Pad.
2. Open a new sketch.
3. Construct a triangle. Once you've constructed the triangle,
manipulate the vertices to create an acute triangle.
5. Using your knowledge of segment bisection, bisect each side of the
triangle to find the midpoint.
6. Join each midpoint to the vertex of the triangle opposite that
midpoint. The three medians created should intersect in one
point. Mark that point.
Using your construction, answer
the following questions on a seperate sheet of paper:
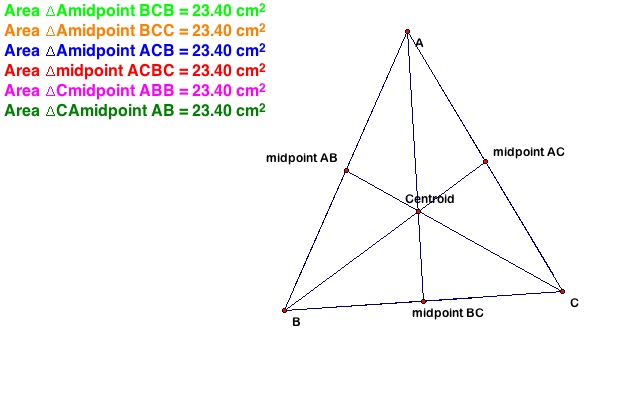
1. Each median divides the
triangle into two halves. How many "half triangles" are there in
your picture?
2. Measure the area of these "half triangles" by highlighting their
vertices, constructing the triangle interior, and measuring the
area. What do you notice about the area measure?
3. Now move one of the vertexes of your triangle. What happens
the the area measures?
4. Make a conclusion about the median of a triangle.
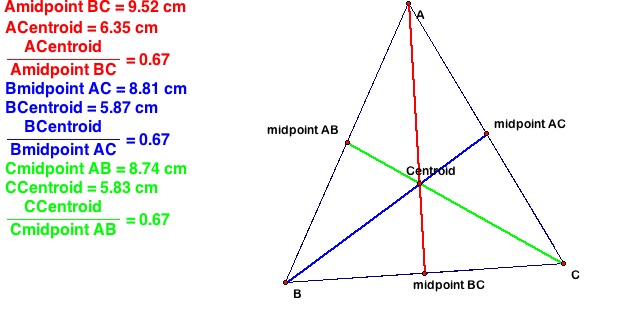
5. Now measure the length of each
median.
6. Also measure the length from each vertex of the triangle to the
centroid.
7. What do you notice about the relationship between this number and
the length of the median?
Summary
of Findings
The centroid of a triangle is the
point of intersection of its medians (the lines joining each vertex
with the midpoint of the opposite side). Each median divides the
triangle into two equal pieces. The centroid divides each of the
medians in the ratio 2:1. That is, the distance from any vertex
of a triangle to the centroid, is two thirds the distance of the median
emanating from that vertex.
Return to my homepage