
Median Problem
by
Rachael Brown
The Problem:
Given three line segments as the three medians
of the triangle. Construct the triangle.
Click here to
open a GSP file that has the problem in it for you to try.
My Solution:
- Construct the triangle that has the three
medians as its sides.
- Construct the centroid of this triangle.
- Construct a circle whose center is the
centroid and whose radius is the distance from the centroid to
one of the vertices (you pick). This is what your construction
looks like so far:

- Extend the median whose vertex you used
to determine the circle into a line. The intersection of the
median and the circle is the midpoint of one the sides of the
triangle you are building. The vertex of the blue and red side
is also a point on the triangle you are building. Use this fact
to create one of the sides of your triangle. Your construction
should now look something like this: (the black segment is one
of the sides of your triangle)
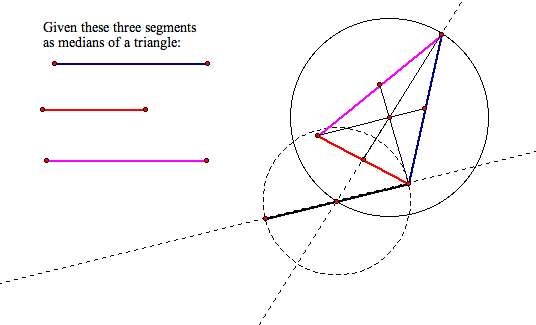
- To get another side we need to look at
the median through the vertex of the blue and ride side of our
median triangle. The length of our median is actually 3/4 of
the size of the side we want. So, we need to construct a circle
whose center is the midpoint of the purple side and it passes
through the centroid of our median triangle. Then extend the
median. The intersection of the median and the circle is the
third vertex of the triangle we're building. Here is a picture
of it:

- Now, we just need to connect the third
vertex to the black segment we already have for the side of the
triangle we are building. Here it is:
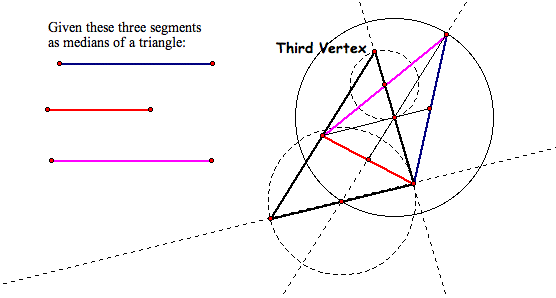
- Click here
to open a GSP file with the above picture in it. Use it to measure
the medians and make sure that we constructed the correct triangle.
Back.





