---

In this write-up, I investigate the locus of the vertices of a parabola when the coefficient of the x-squared term and the constant term have fixed values and the coefficient of x varies.

Let's first look at some graphs when b is varied.

Set a and c equal to 1:

Then draw the graph for b = -3, -2, -1, 0, 1, 2, and 3:

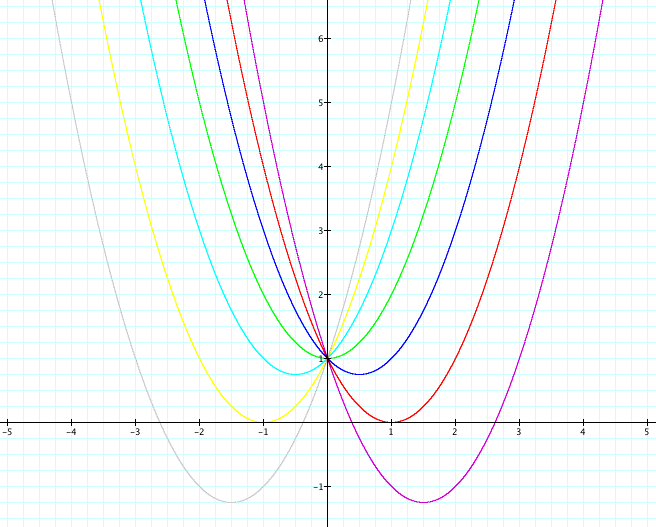
Setting b as n and animating the graph also gives an idea about what the locus of the vertices looks like. Click here to explore.

We can guess that the equation for the locus is

Here is the proof:

x-coordinate for the vertice of a quadratic equation can be found by setting the first derivative equal to 0.

So, 2x + b = 0

x = -b/2

Then, putting this back in the equation gives the y-coordinate:

y = (-b/2)(-b/2) + b(-b/2) + 1 = -(b/2)(b/2) + 1

This shows that

We can generalize this to any quadratic equation

to find the locus of the vertices when a and c are fixed and b is varied.

Again, set the first derivative equal to 0:

2ax + b = 0

x = -b/2a

Insert the x-value in the original equation:

y = a(-b/2a)(-b/2a) + b(-b/2a) + c = -[(b/2a)(b/2)] + c

So, .