Constructing a Circle Tangent to a Given Circle at a Given Point and a Given Line

by Asli Ersoz

The problem is to find two different circles tangent to the following circle at point P and to the following line.

 

I need to find the center of the circle. Here is my construction:

First of all, I know that the center should be on the line which passes through the center of the given circle and the point P.

 

I should find such a point on this line that is equidistant from the point P and the given line.

I construct a line perpendicular to the given line that passes through the center of the given circle. I mark the intersection of this line with the given circle as point B.

 

Then I construct the line through B and P. I mark the intersection of this line with the given line as point C.

Finally, I construct the perpendicular line to the given line at point C and I propose that point D in the following drawing is the center of one of the tangent circles.

 

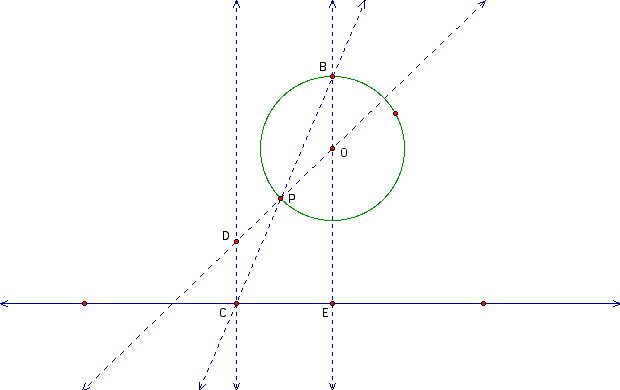
Why is D the center? To prove this I need to show that DC = DP

The following angles are equal: EBP = BPO = DPC

I need to show that angle DCP is also equal to these angles.

Look at angle PCE : It is complementary to both EBP (because BEC is a right angle) and to DCP (because DCE is a right angle).

So, DCP = EBP and hence DCP = DPC.

Therefore, DC = DP and D is the center of our tangent circle. Here it is:

 

 

 

Where is the second circle?

The center again should be on the line connecting the center of the given circle and the point P.

This time, I draw the line connecting P and A. A is one of the intersection points of the given circle and the line through O which is perpendicular to the given line.

I mark the intersection point of this line with the given line as J. Then, I draw a perpendicular to the given line at point J.

I propose that point K is the center of the second tangent circle.

To prove this, I need to show that KP = KJ.

I know that the following angles are equal:

OPA = OAP (Why?)

OAP = KJP (Remember that OA is parallel to KJ.)

So, OPA = KJP.

Hence, KP = KJ.

Here is the tangent circle:

You can click here to observe the tangent circles as point P is taken at different points on the given circle.

Is there any point P for which we can't find two different circles? (Yes.)