Assignment 11: Polar Equations

By Dorothy Evans

Let’s investigate the polar equations below

Purple
Red

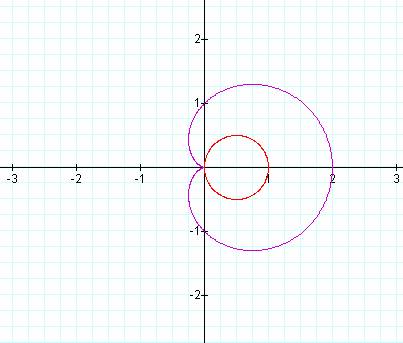
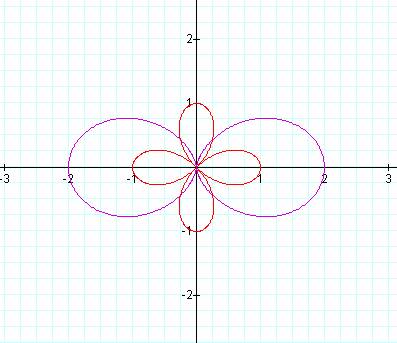
Here is the first case where a = 1, b = 1, and k = 1. As you can see it’s ok, but let’s see when we change k.	Here a = 1, b = 1, and k = 2. As you can see a flower like shape emerges. Notice the length of the red petals are 1 and the length of the purple are 2. Also notice the number of petals. At this point there are 4 red petals and 2 purple. Let’s see what happens next.

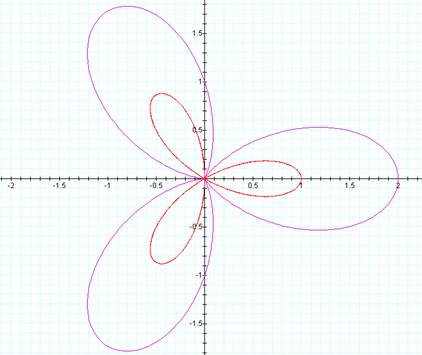
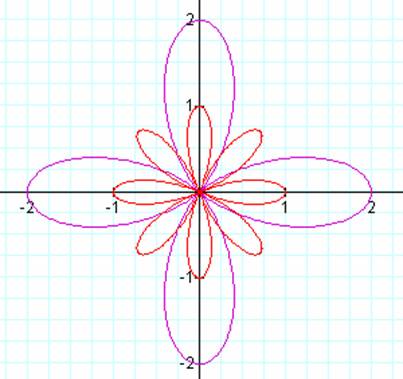
Now a = 1, b = 1, and k = 3. Notice the shape now has 3 petals that are still 1 long in the red and 2 long in the purple. So what do you think k changes? Let’s try another.	Here a = 1, b = 1, and k = 4. It would appear when k is even we get 2k petals in the red graph and k petals in the purple graph. Now let’s see what happens as we change a.

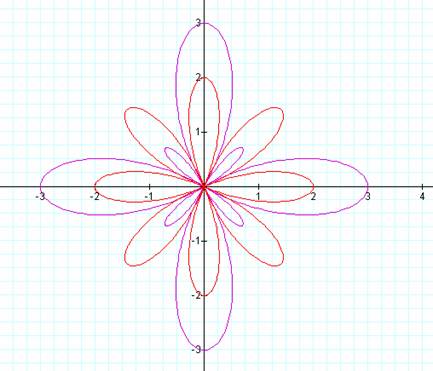
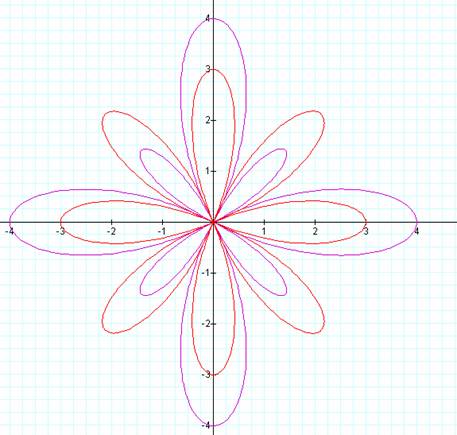
In this case a = 1, b = 2, and k = 4. So, it would appear we now have 2k petals in both the red and purple, but in the purple graph the petals are different sizes. In the red graph the petals are b long and in the purple graph the petals are k-a and a in length.	In this case a = 1, b = 3, and k = 4. The flower got bigger. Notice the larger purple petals are 4. So maybe the length of the larger purple leaves is actually a+b instead of k-a. Also it appears the red are still b in length and the smaller purple petals are not a, but b-a in length. Let’s try another and see if our equations hold true.

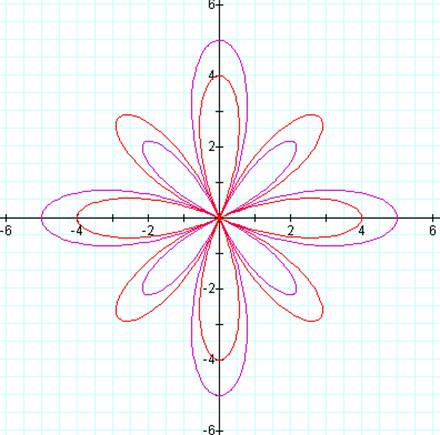
Now a = 1, b = 4, and k = 4. From our previous investigation we hypothesized: # of petals: 2k Size of red petals = b = 4 true Size of larger purple petals = a+b = 1+4 = 5 true Size of smaller purple petals = b – a = 4-1 = 3 true

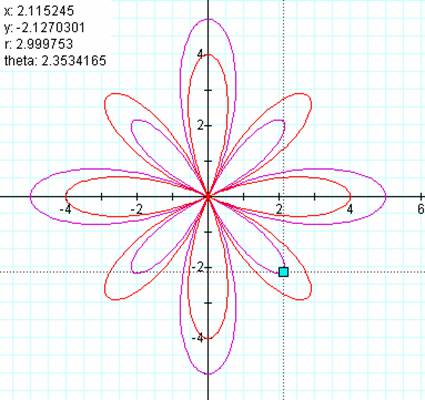
Looks like we got the pattern figured out. Now for those of you wondering how I verified the length of the smaller purple petals because none of them are on an axis. It’s simple, the good old Pythagorean Theorem. I took an estimate of my (x,y) coordinates and calculated the distance to the origin. Now in this case I used an approximation. How would you prove it? For that matter how would you prove any of the distances we hypothesized?

To explore these graphs further click here for the Graphing Calculator file.