Assignment 6

By Dorothy Evans

Problem # 11

11. Consider any triangle ABC. Find a construction for a point P such that the sum of the distances from P to each of the three vertices is a minimum.

I chose this problem because I saw a recent episode on the TV series NUMB3RS that utilized this concept to find a fugitive and I believe this investigation is applicable to a high school geometry course. In the TV show the fugitive had recently been spotted at three locations and the mathematician explained how they could narrow the search by determining the shortest distance from one point to all three of the other points where the fugitive had been spotted. By working on the likely assumption that the fugitive had taken the shortest path to all three locations they could determine the fugitive’s most likely point of origin (where he was hiding). Texas Instruments a sponsor of the show and educators have also created an activity from the show to help students explore this concept and its practical application.

http://www.cbs.com/primetime/numb3rs/ti/activities/Act4_Slippery_Toxin_final.pdf.

This model is also used in logistics problems in determining locations of manufacturing plants, distribution centers, and other locations of interest for companies. The mathematical proof in the concept problem (above) utilizes an equilateral triangle and is therefore a simplified proof of determining the shortest sum of distances from a point to 3 other points. In my example I do not use an equilateral triangle. My first hypothesis was that the shortest distance was one of the centers of a triangle. In my first attempt to validate (while not a formal proof) I convinced myself the centroid was the solution. Here I recreated the problem in GSP and evaluated the sum of the distances manually.

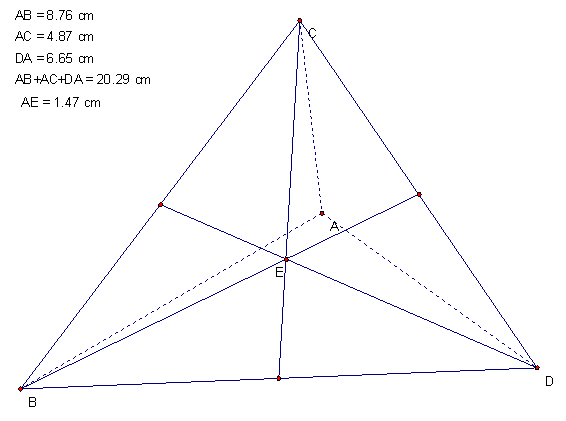
Can you find a contradiction? While the centroid is a close approximation and in an equilateral triangle the centroid would work it’s not the shortest distance in a right triangle or an obtuse or acute scalene triangle. See if you can figure it out before going on. My next hypothesis is that it’s a triangle center I have not yet studied. I believe it’s a center that exists where each of the angles ÛCAD =ÛDAB=ÛBAC= 60 degrees. As you can see this placement would be the centroid if the triangle were equilateral. At this point in time I am still attempting to create a GSP diagram to find this center but have yet to be successful.

An update on my investigation … I have found the name of the center and it is the Fermat point. I am still working on the construction.

For full access to first GSP script for your own investigation click here.