Tangent Circles

By Dorothy Evans

To begin this investigation I found it essential to create the construction on paper to examine the construction process. I then created the construction on GSP. It took several attempts before successfully creating the first tangent circle case (below). In this case, the three green circles represent the tangent circles and the red ellipse is the locus of the center of the third tangent circle (the middle sized green circle.)

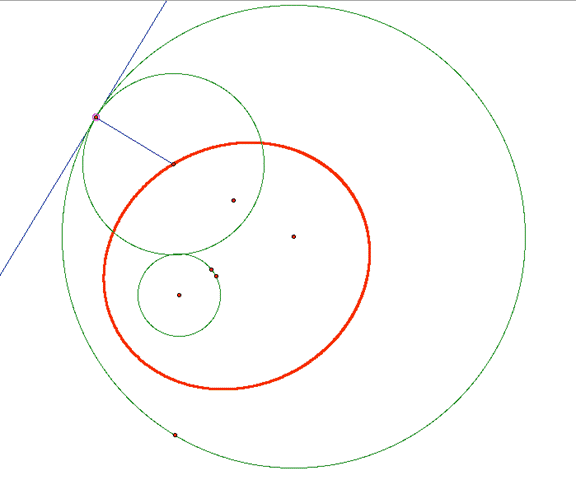
Here is the GSP sketch described above.

After experimenting with several different configurations I found it necessary to label my circles more distinctly to keep track of my different explorations. In this example I have labeled my original circles in blue as circle A and circle B and my tangent circle is the green circle labeled tangent circle.

Since we have explored the locus of points from the center of the tangent circle I was next interested in exploring the locus of points of the midpoint of the segments that formed the base of the key isosceles triangle.

After tracing the midpoint of the isosceles triangle (in purple) you see that the locus of points is a circle.

I then experimented with several different configurations to see if a pattern emerges in the circle. My first observation was that the circle appears to be of the same radius as long as the radius of circle A and circle B remain the same. As circle A becomes larger the locus circle also becomes larger.

I also found it fascinating to see what happens when circle A intersects circle B.

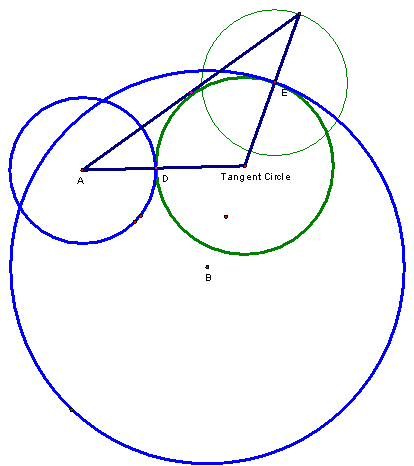
Here you see we still have a circle for the locus. Also notice what happens to the tangent circle as you move around Circle B.

Notice the tangent circle in green is now outside of circle B and you still get a circle for the locus. So what if the radius of circle A is outside of circle B? Will the locus still be a circle? Let’s see.

As you see here the locus is still a circle. It also looks really cool animated. Click here to open the GSP animation.

The next question I have is can we prove the locus of points are a circle and if so where is the center of the circle given circle A and circle B?