Where does c² = a² – b² come from?

Objective: To discover why the relationship c² = a² – b² is true for ellipses. Through a series of steps, we will learn where this relationship comes from.

Step I: r₁ + r₂ = C. What is C?

· Before we learned the distance formula, we were only able to measure the distances between special pairs of points.

o Can you remember what these pairs of points all had in common?

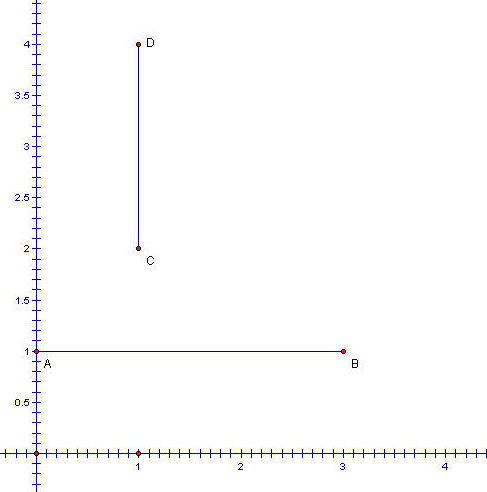
o These pairs of points either shared the same y-value or the same x-value.

§ From the picture above, it is easy to count the distance between point A (0,1) and point B (3,1) since these points share the same y-value. The distance between points A and B, or.

§ Similarly, points C and D share the same x-value. So,.

1. Using our knowledge from above about distances, we want to figure out what the constant distance C is in our definition r₁ + r₂ = C.

o To do this, think about a special point that lies on the ellipse, which we can use to find what C is.

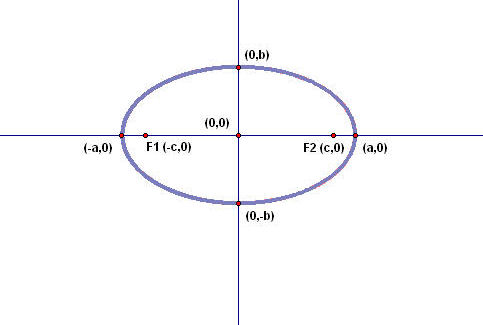
a. What point might be good to use? Mark this point on the above picture, and write its coordinates below. (HINT: Remember, we can easily determine the distances between two points that share the same x-value or the same y-value.)

b. Using the coordinates of the point you chose in part 1a, along with coordinates of F₁ and F₂, find r₁ + r₂. (Your answer will be a distance. Remember that distance is always positive.)

2. Discover the relationship between a², b², and c² using C.

a. Now that you know what the value of C is, can you think about another special point that lies on the ellipse where r₁ = r₂? Draw segments from this point to each focus to represent r₁ and r₂ on the picture below. (Don’t forget what specific distances r₁ and r₂ correspond to. Refer to your quick review sheet if you need a reminder.)

b. Using the point you chose in part 2a, what is the length of r₁? (Keep in mind that r₁ and r₂ are equal at this point on our ellipse.)

c. In your picture, you should have a familiar geometric figure that will lead you to the relationship c² = a² – b².

o What is this figure?

o What well-known theorem is associated with this type of figure?

o How does the relationship c² = a² – b² relate to the figure?