A GEOMETRIC CONSTRUCT
OF A PARABOLA
Assignment 6
by
Gloria L. Jones
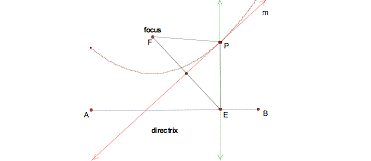
In this assignment the geometric construction of a parabola will be examined whether than from an algebraic perspective. A parabola is the set of all points that are equidistant from a fixed point (the focus) and a line (the directrix).
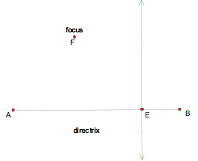
Given a fixed point F for the focus and segment AB for the directrix, we will construct a perpendicular line through a random point E on segment AB as shown:
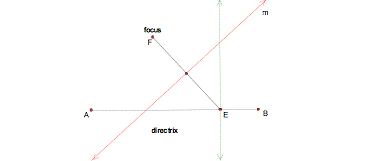
Next, we will form segment FE and construct the perpendicular bisector of this segment (line m):
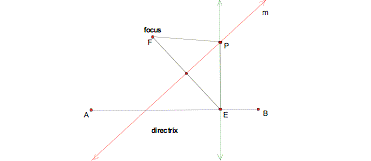
Now we can find the point of intersection of line m and the green line (call it point P). Then connect segment PF and segment PE, the congruent sides of the isosceles triangle formed, thus constructing a point P equidistant from the focus and the directrix:
As point E moves along segment AB, the trace of the equidistant point P is generated. Click here to view animation and trace of point P and resulting parabola. Click here to view trace of the tangent line at point P and resulting parabola.
In the final sketch, GSP is used to generate the locus of points equidistant from a fixed point (focus) and the directrix line: