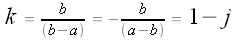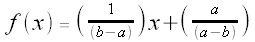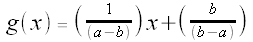We have shown that anytime we have functions
f(x), g(x), and h(x) = f(x)g(x) such that
f(x) is tangent to h(x) at (a,ya)
and g(x) is tangent to h(x) at (b,yb),
we have:
f(a) = 0, g(a) = 1, f(b) = 1, and g(b) = 0.
We have f(a) = 0 and f(b) = 1, so
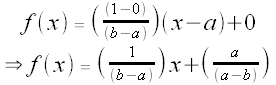
Thus, 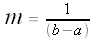 and
and 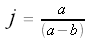
We also have g(a) = 1 and g(b) = 0, so
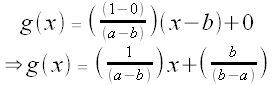
Thus, 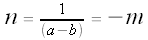 and
and 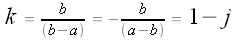
So we have
|
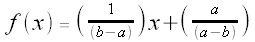
and
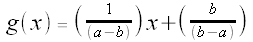
|
In this Graphing Calculator file, you can enter two x-values a and b,
and the file will graph two linear functions and their product
such that the linear functions are tangent to their product
at (a, ya) and (b, yb).
<< Previous (Intro)
Return to my page
Return to EMAT 6680 page

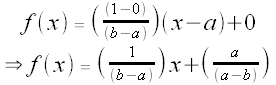
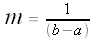 and
and 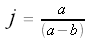
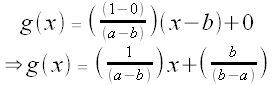
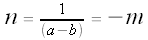 and
and