
Quadratic Functions
|
|
Again, consider the quadratic function
f(x) = ax2 + bx + c
Suppose b and c are constant, and let a vary.
What does the locus of the vertex look like as a varies?
Make a conjecture about some properties of the equation describing the locus of the vertex as a varies. What shape is the locus? How do b and c figure into the equation? Be sure to look at the case when b = 0.
Now that you've made a conjecture, let's rigorously determine an equation for the locus of the vertex as a varies.
We have shown that the vertex of the parabola is located at
Let Since a is varying, we want to find the y-coordinate of the vertex in terms of only x, b, and c. In order to "swallow up" all of the a's in the equation, we have to use x's (since x depends on a, but b and c don't).
There is an a in the denominator of
So What is s?
So And clearly c is already in terms of only x, b, and c.
Thus, the locus of the vertex as a varies is
(Be careful! Note that when b = 0,
Does this match your conjecture?
Click here to see a Graphing Calculator animation as a varies,
Check the interesting b = 0 case as well. What do you see? Click here to continue and see what happens when b varies.
|


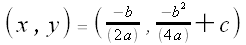
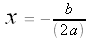 . This is the x-coordinate of the vertex.
. This is the x-coordinate of the vertex.
 , the first term of y, and there is an a in the denominator of
, the first term of y, and there is an a in the denominator of  for some s that is in terms of b and c.
for some s that is in terms of b and c.



 and
and 