
Parabola Equation
|
|
Let's describe our construction algebraically. Let (a,b) be the coordinates of the focus F, and let y = y0 be the equation describing the directrix d (for simplicity, let's only look at horizontal directrices).
Finally, let (x0,y0) be the coordinates of X.
1: Draw
We will only need the slope m of this line. We have:
2. Let M be the midpoint of
h goes through M, whose coordinates are
3. Draw k, the line which is perpendicular to d and goes through X.
d is horizontal, so k must be vertical.
4. Let P be the point at which h and k intersect.
The intersection of h and k is simply the point on h when x = x0. This point is (x0,yi), where:
Now, letting the point X vary on d (i.e., letting x0 vary in R), we have that the parabola is the set of points:
So the parabola is the curve in the plane described by
|
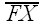



 , by the midpoint formula.
, by the midpoint formula.






