
The Simson Line
|
||||||||||
|
Hopefully, your investigation yielded something like this:
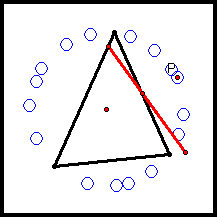
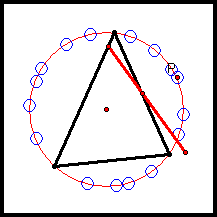
The blue circles seem to lie on the circumcircle of the triangle.
So if the pedal point P lies on the circumcircle of ΔABC, it looks like we have a Simson Line. Let's prove it!
Let P be any point on the circumcircle of ΔABC, and let D, E, and F be the vertices of the pedal triangle for pedal point P.
Draw in segments
Look at quadrilateral ACPB.
A, C, P, and B all lie on a single circle, so
Now look at quadrilateral AEPD.
And the sum of the interior angles of a quadrilateral is always 360°, so we have
By (1) and (2), we have
Now I want to show that γ = σ
I claim that B, D, F, and P lie on a single circle.
First, take a look at this GSP animation.
Now look at
What do you see?
Those two angles are congruent, since they are both right angles!
Now look at angles γ and σ. Again, just like the angles in our animation, they are angles which subtend a given segment (namely,
So γ = σ
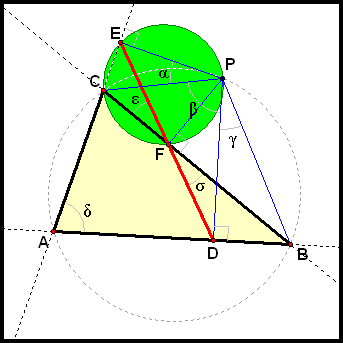
Similarly, using points C, E, P, and F (see diagram below), we have
Let's review what we know so far:
By (3), (4), and (5), we have
So ε = σ
So Thus, D, E, and F are collinear. Q.E.D.
We have shown that anytime the pedal point P is on the circumcircle of ΔABC, then we have that the pedal triangle is a degenerate triangle, or a Simson line. Check out this GSP file to see what happens as we trace the [infinitely extended] Simson line as P travels around the circumcircle. Pretty cool, huh?
|
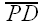 ,
, 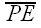 , and
, and 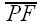 , and label some angles as shown:
, and label some angles as shown:
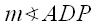 = 90°, and
= 90°, and  = 90° (by construction, since ΔDEF is a pedal triangle).
= 90° (by construction, since ΔDEF is a pedal triangle).
 δ + 90° + (β + α) + 90° = 360°
δ + 90° + (β + α) + 90° = 360°
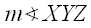 is a given value.
is a given value.
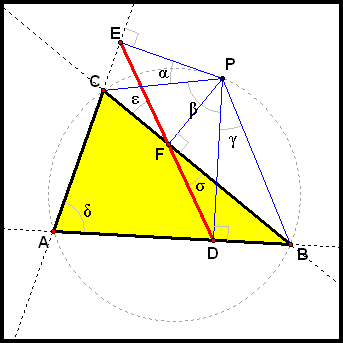
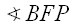 and
and 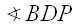 in our original diagram.
in our original diagram.
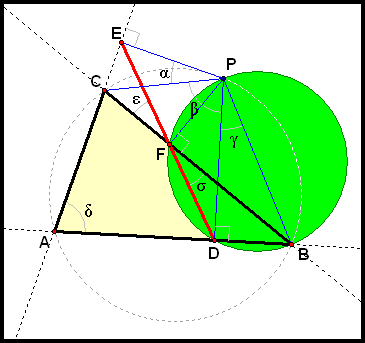
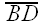 ) and whose vertices lie on the same circle as the endpoints of that segment.
) and whose vertices lie on the same circle as the endpoints of that segment.
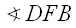 and
and 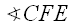 are vertical angles.
are vertical angles.