Oktay Mercimek, EMAT 6690
A Cone Half Full
Oktay Mercimek, EMAT 6690
A Cone Half Full
Consider a right circular cone with diameter of 12 cm for the base and altitude of 16 cm. If the cone is held with its vertex down and water placed into it until it is half full, what is the depth of the water?
Image 1
Let's look how can we find a general solution for this problem using spreadsheet.
I prefer to use variables instead of exact values, therefore extending this problem to any value will not be a problem.
Then we can use this spreadsheet file not only for this purpose but also for other purposes.
Lets start with how can we define the volume function of cone in the spreadsheet file
First we need to know which values we needed. As you know from the geometry course the volume of the cone is
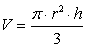
Then we need Pi , r (radius of the cone) and h (altitude of the cone).
But the main problem is not equation of the volume of the cone. The problem is the radius of the cone when we cut it with a parallel plane
As you see it, radius decreases when the altitude decreases.
We know AB is parallel to DE, then that makes
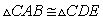
therefore
.
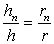Since we know what the h and r are and we cut the cone at a special altitude
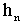, we need to learn what is the value of the
.
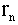So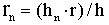 
.
Now how we can use these formulas in spreadsheet. My example is in Excel format.
| A | B | C | D | E | F | ||
| 1 | pi= | 3.14159 |  = |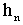
5 | <---An arbitrary value between 0 and 16 | ||
| 2 | r= | 6 | = |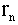
=(E1*B2)/B3 | |||
| 3 | h= | 16 | |||||
| 4 | |||||||
| 5 | Volume of the Original Cone | =(B1*B2^2*B3)/3 | Volume of the Small Cone | =(B1*E2^2*E1)/3 | |||
| 6 |
Click HERE (A Half Cone Full-1.xls) to see the script in Excel file.
As you can see that script computes the new radius using the new altitude value that we entered to the cell E1.
This script may help if you wonder what happens when you cut your cone with a specific altitude.
What we should we do to find the volume of upper part of the cone, Conical Frustum?
It is clear that this script doesn't solve our problem so much, so we need a
script that examine several values of
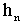that helps us determine the
correct altitude to solve the question.
What can we do?
We can examine the volume of the small cone for values 1,2, ... , 16 so we have data to construct information.
To do that,
| A | B | C | D | E | F | ||
| 1 | Pi= | 3.14159 | h(new) values | r(nev) values |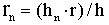
Volume for h(new) value | ||
| 2 | r (radius)= | 6 | 1 | =(D2*B$2)/B$3 | =(B$1*E2^2*D2)/3 | ||
| 3 | h= | 16 | =D2+1 | =(D3*B$2)/B$3 | =(B$1*E3^2*D3)/3 | ||
| 4 | =D3+1 | =(D4*B$2)/B$3 | =(B$1*E4^2*D4)/3 | ||||
| 5 | =D4+1 | =(D5*B$2)/B$3 | =(B$1*E5^2*D5)/3 | ||||
| 6 | ... | ... | ... |
Now what is an easy way to do it?
In excel you can copy a cell and paste it to another cell, Excel automatically arranges formulas for the new cell.
It sometimes causes problems, such as the difference between cell E2 and E3.
you can see that D's are changing but B2 and B3 don't change. Because the
variable in this formula is only h(new),
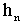, and B2 (radius value) and
B3(altitude of the cone) are fixed values, so we put $ sign before 2 in B2 and
before 3 in B3, This is a shortcut in Excel, What it does is simply it doest
change the 2 and 3 in these boxes when you copy it to another cell in the same
column.
Steps to make this table in Excel:
Step 1. enter "1" to D2 , and "=D2+1" to D3. This makes D3=2. then go to the lower right corner of D3 when the D3 is selected as in the image below
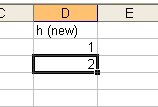
When you reached to the lower right corner, Arrows becomes Plus sign.
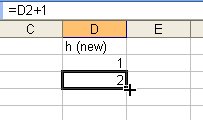
when It is plus sign, click the mouse and hold it, then drag it to the lower cells
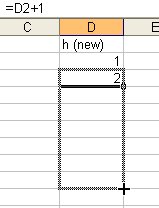and the result
is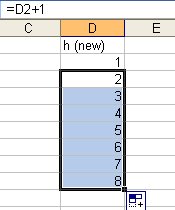 
We automatically copied down to the new cells, If 8 is not enough then click the lower right corner of the Cell that has 8 in it and drag it to lower cells
Step 2. Enter "=(D2*B$2)/B$3" to E2 and
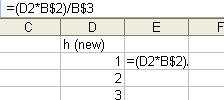
copy it down as in the step 1.
it becomes like this
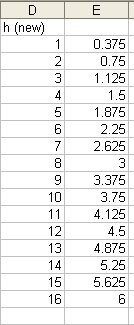
Step 3. Enter "=(B$1*E2^2*D2)/3" to F2 and copy it down.
we can clearly see that for an h value between 12 and 13, the volume of new cone can be half of the original cone. half of the original cone must be approximately 603/2=301.5.
Step 4. How can we find more precise result?
Since we know that the h value we are looking for is between 12 and 13, we can start to examine h values from 12 with 0.1 increments.
We can simply do that by changing D column values we entered in step 1
We can enter "12" to the cell D2 and "=D2+0.1" to cell D3 and then copy it down as in he picture below
Now we can conclude that for h=12.7 , volume of the half cone is very near to the value of half of the original cone.
