Elliptical Explorations

by Oktay Mercimek

I would like to explore the third investigation from assignment 10 and that is

For various a and b, investigate

.

 

For a=1 and b=1, the equation is       for   (purple curve) and its graph is

 

 

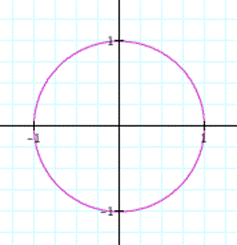
It seems like a circle. Let's try it for more a and b.

For  a=1 b=2 ,it is     for   (red curve)

 

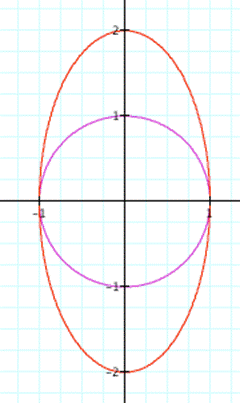
and this time it seem like an ellipse that intersects x-axis at points -1 and 1 , and intersects y-axis at -2 and 2.  In the first one a and b was 1 and intersection points was

(-1,0) , (1,0) , (0, -1) and (0,1)    ( a=1 and b=1)

(-1,0) , (1,0) , (0, -2) and (0,2)    ( a=1 and b=2)  for the second graph

 

Can we generalize points as

(-a,0) , (a,0) , (0, -b) and (0,b) for a>0  and b>0  ?

 

Let's try it for a=3 and b=4        for  (blue curve)

 

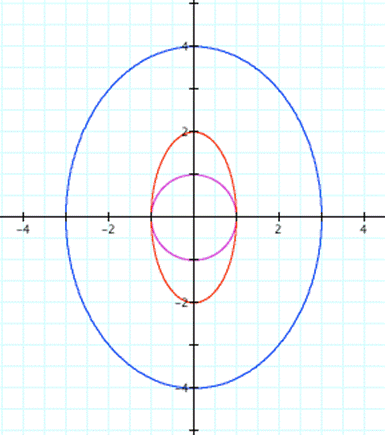
Points are (-3,0) , (3,0) , (0, -4) and (0,4)     a=3 and b=4 , Generalization holds for this one. Let's change a and b with each other.

 So make it a=4  and b=3       for    (green curve)

 

 

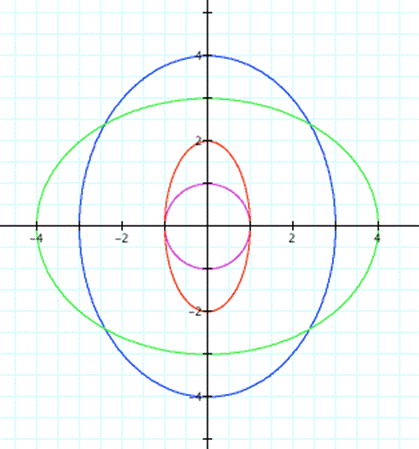
Since our generalization also holds for this example , let's look at algebraic side of this equation to see whether our generalization holds for all natural numbers.

 

Our equation is  for .

 

Let's find algebraic form of this parametric equation.

Most common relationship between sin and cos function is .

To make our equations like this we need to take square of both sides in the parametric form

So it is

 

 

 

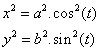
sin and cos functions must have same coefficient so multiply first by and second by

 

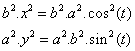
Now we can sum up both sides

 

 

 

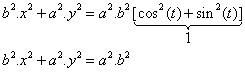
Dividing both sides with  gives us

 

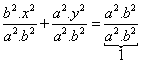
After simplification,

 

 

 

This is obviously an ellipse equation so we can say our assumption about parametric equation is true.

This ellipse intersects the x-axis at (-a,0) and (a,0) and y-axis at (0,-b) and (0,b)

so we just learned that for is actually a ellipse equation.