Part A: Bouncing Barney

A. Bouncing Barney. We discussed this investigation in class. Your challenge now is to prepare a write-up on it, exploring the underlying mathematics ideas and conjectures.

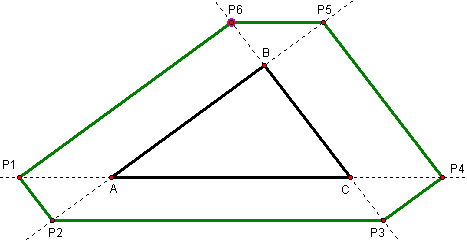
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.

Who's your favorite Barney?

To solve this problem, I first made this GSP sketch which models poor Barney's situation. It seems that if Barney (who starts at point P1 and progresses to P6 before he returns to P1 again) always touches the same six points on the triangle before he reaches his start, no matter where he begins (except for two special cases I will discuss below). Can we prove this? You bet!

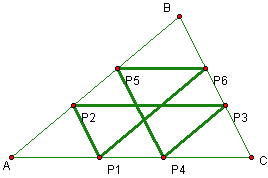
P1P2 is parallel to BC, so by the angle angle similarity theorem, triangle AP2P1 is similar to triangle ABC. Therefore length(AP2)/length(AB) = length(AP1)/length(AC). Similarly, since P2P3 is parallel to AC, triangle BP2P3 is similar to triangle BAC, and so length(AP2)/length(AB) = length(CP3)/length(BC). Following this pattern we find that:

length(CP3)/length(BC) = length(CP4)/length(AC),
length(CP4)/length(AC) = length(BP5)/length(AB),
length(BP5)/length(AB) = length(BP6)/length(BC),

We are trying to prove that the next point, P7 is equal to P1. Still following the pattern, we get:

length(BP6)/length(BC) = length(AP7)/length(AC).

Our long chain of equalities, however, tells us that length(AP1)/length(AC) = length(AP7)/length(AC). Since P1 and P7 both lie on the segment AC, P1 = P7, and so Barney is in a six stop cycle, unless he started on a point mentioned in the two cases below.

Case 1: Barney starts on a midpoint of any side of the triangle, say the midpoint of AC.

If Barney walks parallel to BC, he will reach the midpoint of AB, because the line connecting the midpoints of two edges of a triangle is parallel to the third edge. Similarly, when Barney leaves the midpoint of AB, he will next reach the midpoint of BC, then the midpoint of AC, where he started. If Barney leaves from a midpoint, he thus only gets to see two points. He would have a much more pleasant trip if he took a scenic route not beginning at a midpoint. Poor Barney.

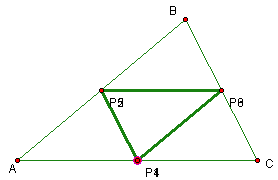
Case 2: Barney starts on a vertex of the triangle

In this case Barney walks around the edges of the triangle.

If Barney starts on a point not on a point on the line through AC but not on the segment AC and moves parallel to BC, he must go towards AB if he wishes to change his direction again. If he does this, he will see six different point, as in the usual case. The proof of this fact is similar to the proof above.