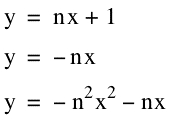Problem #3: This problem asked to find two linear functions f(x) and g(x) such that their product
h(x) = f(x).g(x)
is tangent to each of f(x) and g(x) at two distinct points. My two linear equations that I used and their product are as follows:
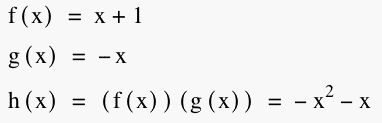
Here is the graph:
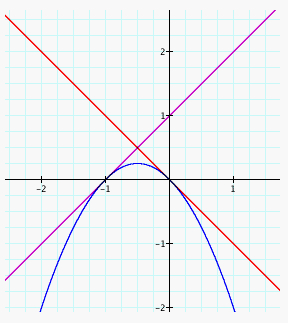
One finds out upon investigating this problem that the only way this problem will work is if these four things occur:
1. The graphs of f(x) and h(x) meet at a specific value of x. Let x = a.
2. f'(a) = h'(a)
3. The graph of g(x) and h(x) meet at a specific value of x. Let x = b.
4. g'(b) = h'(b)
Because the derivate of h(x) will be equal to the derivate of the linear equations at the given location in #2 and #4, we know that the graph of h(x) is tangent to the graphs of the linear equations at these two points.
Check the solution:
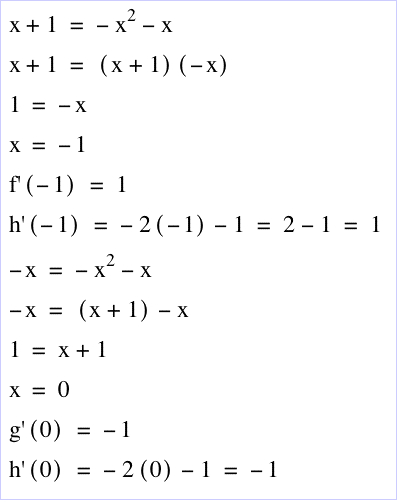
An interesting exercise: Plug in these equations and let n vary from -10 to 10. Enjoy!!