
Assignment 11 Write-up

Investigate r = a + b cos (kq)
When a and b are equal and k is an integer, the "n-leaf rose" is formed. Here a = b = 2 and k = 3.
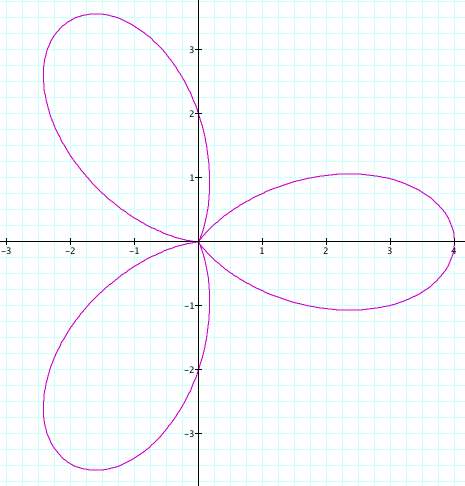
Let's see what happens when a and b are not equal. We'll let a = 5 and b = 3.
 As
you can see, the leaves don't meet in the center when the numbers
aren't equal. Let's see what happens if b = 5 and a = 3.
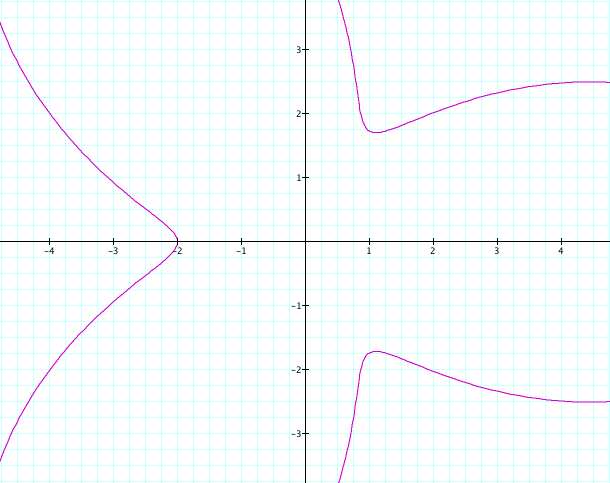
As
you can see, the leaves don't meet in the center when the numbers
aren't equal. Let's see what happens if b = 5 and a = 3.
 Wow,
did you expect this to happen? Not only have the leaves met in
the center again, but there are 3 smaller leaves imbedded in the
original ones. Let's see what happens if we just change the value
of k to 5.
Wow,
did you expect this to happen? Not only have the leaves met in
the center again, but there are 3 smaller leaves imbedded in the
original ones. Let's see what happens if we just change the value
of k to 5.
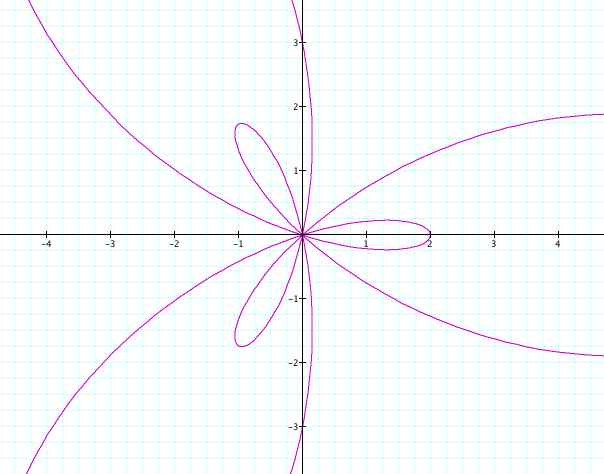
 OK,
now I'm beginning to make a few connections. Are you? Have you
noticed the only thing that changed about this graph is the amount
of leaves? How many small ones are there and how many large ones
are there? That's right. . .5! The same number that k is! Also,
have you noticed yet that there is always one leaf that is symmetrical
around the positive x axis? Let's try another one. What if k =
-5?
OK,
now I'm beginning to make a few connections. Are you? Have you
noticed the only thing that changed about this graph is the amount
of leaves? How many small ones are there and how many large ones
are there? That's right. . .5! The same number that k is! Also,
have you noticed yet that there is always one leaf that is symmetrical
around the positive x axis? Let's try another one. What if k =
-5?
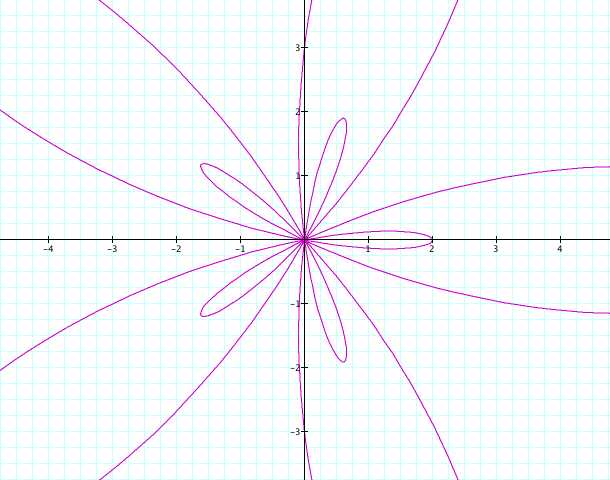
 Did
you expect this? There is no change! Do you think that it's because
changing k from positive to negative simply makes the graph be
drawn in a clockwise direction instead of a counter-clockwise
direction? It makes sense to me; every point would still be plotted,
but in "reverse order"! What if a and b are both negative?
Try a = -3 and b = -5.
Did
you expect this? There is no change! Do you think that it's because
changing k from positive to negative simply makes the graph be
drawn in a clockwise direction instead of a counter-clockwise
direction? It makes sense to me; every point would still be plotted,
but in "reverse order"! What if a and b are both negative?
Try a = -3 and b = -5.
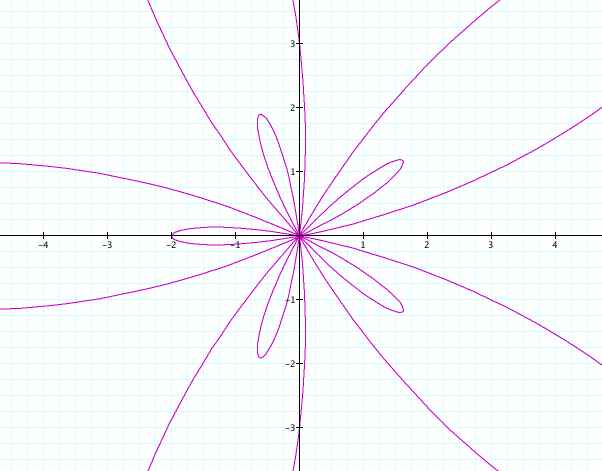 Aha!
Notice that there is no longer a leaf symmetrical across the positive
x-axis, but the negative x-axis! The whole graph seems to have
flipped over the y-axis! Let's see what happens if we completely
take out the a term and leave b = -5.
Aha!
Notice that there is no longer a leaf symmetrical across the positive
x-axis, but the negative x-axis! The whole graph seems to have
flipped over the y-axis! Let's see what happens if we completely
take out the a term and leave b = -5.
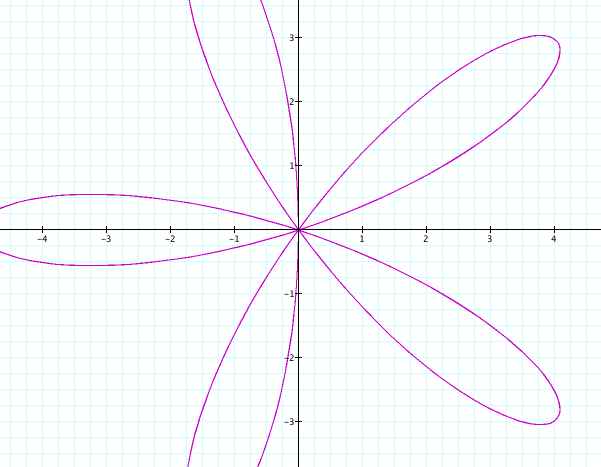 How
about that! It looks like the smaller leaves combined with the
larger leaves to make "medium-sized" leaves!
How
about that! It looks like the smaller leaves combined with the
larger leaves to make "medium-sized" leaves!
There are many other ways to play with polar equations. Feel free to explore opportunities that I may have left out!