Assignment 2 Write-Up

Billy Poe

1. Construct graphs for the parabola

for different values of a, b, and c.

Part 1:

Let's look at the equation

and let a have the following values: {-10, -5, 0, 5, -10}

so here are our new equations:

and here are our graphs:

 

 

First of all, notice that if a is positive, then the graph opens up and if a is negative then the graph opens down. Also, as | a | gets larger, the graph gets skinnier or looks like it is stretched.

Part 2

Let's look at the equation

and let b have the following values: {-4, -2, 0, 2, 4}

so here are our new equations:

and here are our graphs

 

Notice first that the graphs are reflected around the y-axis. For example, the purple graph is reflected in the light blue graph and the red graph is reflected in the green graph. However, note the interesting fact that if b is positive then the vertex has a negative x value and if b is negative then the vertex has a positive x value. Lastly, notice that all graphs go through the point (0, 2). This is because when the x-value equals 0, then the y-value equals c, which in this case is 2.

Part 3

Let's look at the equation

and let c have the following values: {-4, -2, 0, 2, 4}

so here are our new equations:

and here are our graphs

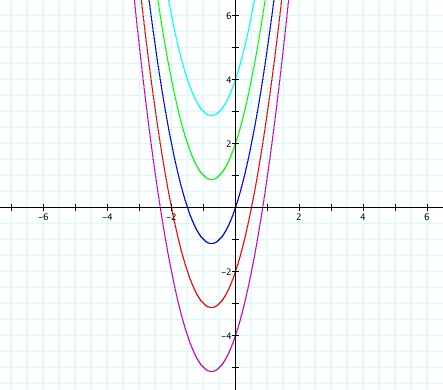
Notice first that each graph has the same x-value for its vertex: -3/4. The reason for this is because each equation is the same except for the constant and the constant plays no part in determining where the minimum or maximum is in a graph. Minimums and maximums are determined by finding the first derivatives of an equation. In this case, each graph has the same derivative: 4x + 3 = 0 which yields x = -3/4. So, if we start with our blue graph where c = 0, we see that each graph shifts up or down depending on its c value. For instance, the light blue graph is 4 units above the blue graph because c = 4.

Return