
Assignment 3 Write-up

Now consider the locus of the vertices of the set of parabolas graphed from
![]()
Show that the locus is the parabola
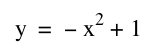
First of all, you may be asking yourself, "What is a locus, exactly?" Let's just be clear on the definition.

Now, what do we know about vertices of a parabola?
1. They are either a relative maximum or a relative minimum value.
2. The slope of the graph is positve on one side of a vertex and negative on the other side.
3. The f ' (x) = 0 at the vertex.
So, a locus of the vertices of the set of parabolas graphed from our given equation would somehow be connected to the derivative of the equation.
![]()
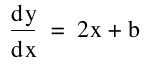
Now, remember, we have to find each vertex of the graph. So we have to set the derivative equal to 0 and solve for b.
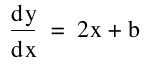
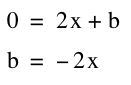
So this is the relationship with each b value and the corresponding x value at the vertex. Now just plug in b into the original equation.
![]()
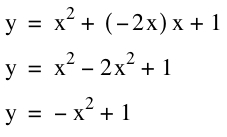
So this is the equation for the locus of the vertices of our given equation. Check it out!