A Proof

Given: Two fixed circles where one circle is in the interior of the other and a tangent circle tangent to the larger fixed circle at a given point such that the non-tangent points of the smaller given circle are in the interior of the tangent circle.

Prove: The locus of the centers of all possible tangent circles constructed in this manner is an ellipse.

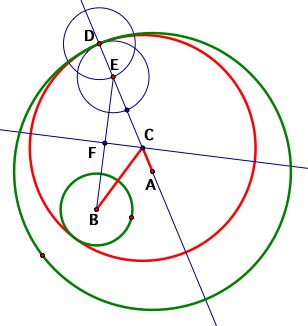
Consider the diagram below.

In order for the locus of the centers of the tangent circles is an ellipse, the sum of the distances from the two foci A and B to the center of the tangent triangle C must be constant for any point of tangency D. To summarize, AC + BC must be constant.

To show that the sum is constant, it is helpful to first show that Triangle EFC is congruent to Triangle BFC. This can be accomplished by asserting that Segments EF and BF are congruent (due to F being the midpoint of Segment EB), Segment CF being congruent to itself (reflexive property) and Angles EFC and BFC being congruent (since Lines FC and EB are perpendicular, both angles are right angles and, therefore, congruent). Thus, Triangle EFC is congruent to Triangle BFC by SAS.

From these congruent triangles, corresponding Segments CB and CE are congruent. Using substitution, AC + BC becomes AC + CE which equals AE.

Is AE constant? Since AE = AD - DE and both AD and DE represent the respective radii of the fixed circles, it can be established that AE is constant. Thus, for the possible points D on Circle A, the locus of C is an ellipse. QED : )