Suppose that on a remote island, the members of a tribe are
engaged in three occupations:
1) farming, 2) manufacturing of tools and utensils, and 3) the weaving
and sewing of clothing.
Assume that initially the tribe has no monetary system and that
all goods and services are
bartered.
The tribe divides the goods and services up as follows:
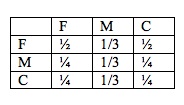
Farmers:
The farmers keep half of their produce and give one quarter of their produce to the manufacturers and on quarter to the clothing producers.
Manufacturers:
The manufacturers divide the goods evenly among three groups, one third goes to each (including themselves).
Clothing weavers:
The group producing clothes gives half of the clothes too the
farmers and divides the other
half evenly between themselves and the manufacturers.
This is represented by a table:

The first column of the table indicates the distribution of
the goods produced by the farmers,
the second column indicates the distribution of the manufactured
goods, and the third
column indicates the distribution of the clothing.
As the size of the tribe grows, the system of bartering becomes
too difficult and, the island decides to institute a monetary system
of exchange. For this simple economic system, assume that the prices
for each of the three types of goods will reflect the
values of the existing bartering
system.
Your assignment is to develop a system of monetary exchange. Then assign values to the three types of goods that fairly represent the current bartering system.
<>This problem can be turned into a linear system using a model that was originally developedNow open up a new document in javabars.
Draw three different bars, make them three different colors and label the bars x1, x2, x3.
Draw three equal sized mats, label these as farming, manufacturing , and clothing.
farming=x1
manufacturing=x2
<>clothing=x3Divide the bars up according to how much goes to each of the three occupations. (i.e. farmers give 1/2 to themselves, 1/4 to manufacturing, and 1/4 to clothing.)
Place the proper proportions in each mat as given by the rows in the table.1) Write an equation for the farming mat,
showing where each piece on the mat came from. (Remember what x1,
x2, and x3 stand for. )
2) What does this mat represent (in
total)?
3) What should this mat be equal to?
4) Self Check: Now reread the blue
paragraph above. Does your answer match?
Answer the first three questions for the
other mats: manufacturing and clothing. Remember to show in your
equation where each piece on the mat came from. Take a moment to
think about what each mat is representing and what each mat should
equal.
The three equations you should now see from what we just did are:
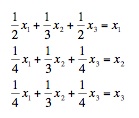
Switch now to Graphing calculator.
Input these three equations we got from javabars substituting
x1=x, x2=y, and x3=z, and graph these equations.
Answer these
questions on a separate sheet of paper:
1) Do the planes intersect at a point or a line?
2) What is the significance of
this? How many solutions will this system of equations have?
3) How can you manipulate these three equations to solve them? (hint matrix form)
4) Once the system is in matrix form,
what do you have to do in order to find
the ratio between x1, x2, and x3?
5) Using your findings, develop a
currency system for the island. Assign prices to clothing,
manufacturing, and farming.