

Barney is in the triangular room with vertices
A, B, and C. He walks from a point on segment BC parallel to segment
AC. When he reaches segment AB, he turns and walks parallel to
BC. When he reaches segment AC, he turns and walks parallel to
AB. Prove that Barney will eventually return to his starting point.
How many times will Barney reach a wall before returning to his
starting point? Explore and discuss for various starting points
on line BC, including points exterior to segment BC. Discuss and
prove any mathematical conjectures you find in the situation.
Let explore Barney's adventure according to the directions above.
|
|
|
 |
 |
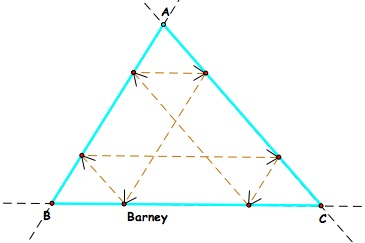
Since Barney walks on a path that parallel
to each segment, he will always return to the starting point.
Clearly, we can see that Barney touches the segments and exterior
of the triangle five times before returning to his original position.
From the pictorial representation of his starting point on segment
on BC, it looks as though his path has similar triangle at each
vertex.
There are several way to prove that this conjecture holds true. We will explore one way using the interior of the triangle ABC while comparing it to the segments of the triangle. Look at the first triangle above closely. Do you see three parallelograms? Since Barney's path created parallelograms, let's see if there is any relationship among them and the triangle ABC.
 |
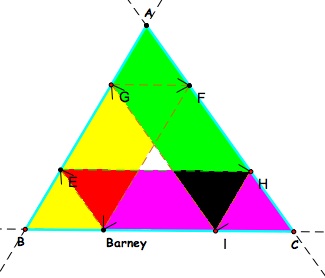 |
The perimeter of the parallelograms, excluding
the segments that are part of the triangle, are equivalent to
the perimeter of the triangle. This illustrates that Barney returns
to the starting points on segment BC because his bouncing path
is the same measure of the triangle.
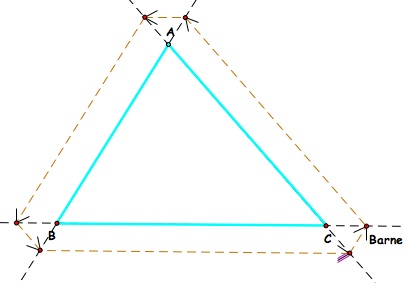
What happens if Barney's starting point is point B or C?
If he begins at the points B or C, he will also return to his original resting place. Click here to see a diagram.
What happens if Barney's starting point outside to the triangle?
If Barney's starts at a point P outside to the triangle, not an element of lines AC, AB, or BC, then Barney will never return to his original position. Click here to see a diagram.
What do you think will happen starts bouncing from a point in the interior of the triangle, such as the centroid? Give it a try.