---

Assignment Eleven

---

Here, we will compare and . Before doing so, we will explore r = bcos(k theta).

Predict how the graph of r =b cos(k theta) will look. Click here to check your assumption. Now, Let's examine the polar equation when b = 0, 1, 2, 3, 4, where k =1.

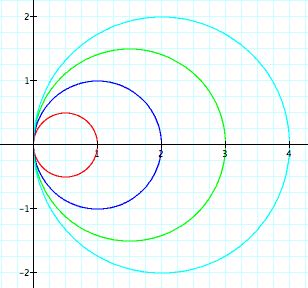
It seems as though that the values of b effect the diameter in each circle. In other words, b = diameter, when k = 1. When compare to r = a + b cos(ktheta), it seems, here, that the graph was translated over the x-axis.

Now, we should experiment with various values of k. Consider the equation when k = 2, 3, 4, 5, 6, 7 and b = 1. How do these graphs compare to where k was equal to the integers, 0 through 6?

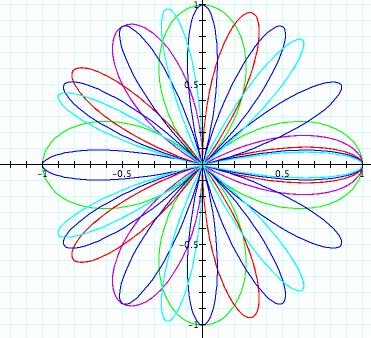
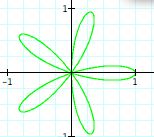
From the graph above, it is hard to investigate what happens as the values of k change, where b = 1; however, it seems as though the domain and range goes from -1 to 1 for each value k. We need to separate the graphs to further examine the values of k. Let's see what happens when k is even and odd.

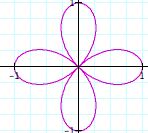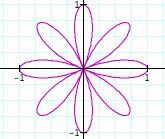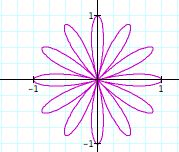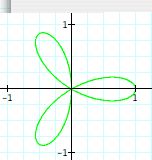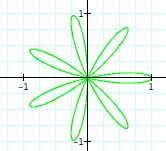Notice: Separating the graphs based on the odd and even values of k has helped us to investigate the polar equations even more. By examining the graphs, what conclusions can you draw? There seems to be some difference between the number of n-leaf rose when k is even and odd and b remains equal to one. When k is even integer, the number of pedals double the value of k. In other words, if k= even number, then there will be 2k pedals or leaves on the rose, 2k-leaf rose. When k is an odd integer, the number of pedals equals the value of k. Thus, we will have a n-leaf rose. This is quite similar to polar equations that we investigated in the beginining.

Click here to see an animation of different values for k.

What if cos(ktheta) is changed to sin(ktheta)?

Return