Parametric Equations

Assignment 10

Problem #7

By Erin Cain

In this problem we are asked to do the following:

Write parametric equations for a line segment that goes through the point (7, 5) with a slope of 3. Graph the line segment using your equations.

This is a good problem to give students when learning about parametric equations. The first thought a student might have is to go ahead and find the equation of the line using the point-slope form. We need to recall that the point-slope form looks like the following:

y – y₁ = m(x – x₁)

where m = slope and (x₁, y₁) is the given point

Therefore we can substitute in the given values for the certain variables and solve in the following way.

y – 5 = 3(x – 7)

y – 5 = 3x – 21

y = 3x – 21 + 5

y = 3x – 16

So we now have our equation of the line through the point (7, 5) and with a slope of 3 to be y = 3x – 16.

A parametric curve in the plane is a pair of functions

x = f(t)

y = g(t)

where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t and your work with parametric equations should pay close attention the range of t. In many applications, we think of x and y "varying with time t" or the angle of rotation that some line makes from an initial location. In this case, we are not dealing with curves; instead we are working with a single equation for a line. In order to write the equation of the line in parametric form, we still must have two equations and in t. When looking at the equation y = 3x – 16, we see that we have an equation for y, but it is not in terms of t. So how can we change it so we can use it in a parametric equation? Well, we can substitute t in for x. This would then give us our equation for y in terms of t; y = 3t – 16. Now we need an equation for x in terms of t. Due to the fact that we substituted t in for x, we know that x must equal t. Therefore, our equation for x will be x = t. Hence are parametric equations for a line that goes through the point (7, 5) and that has a slope of 3 is:

x = t

y = 3t – 16

We can graph this to see if these equations work.

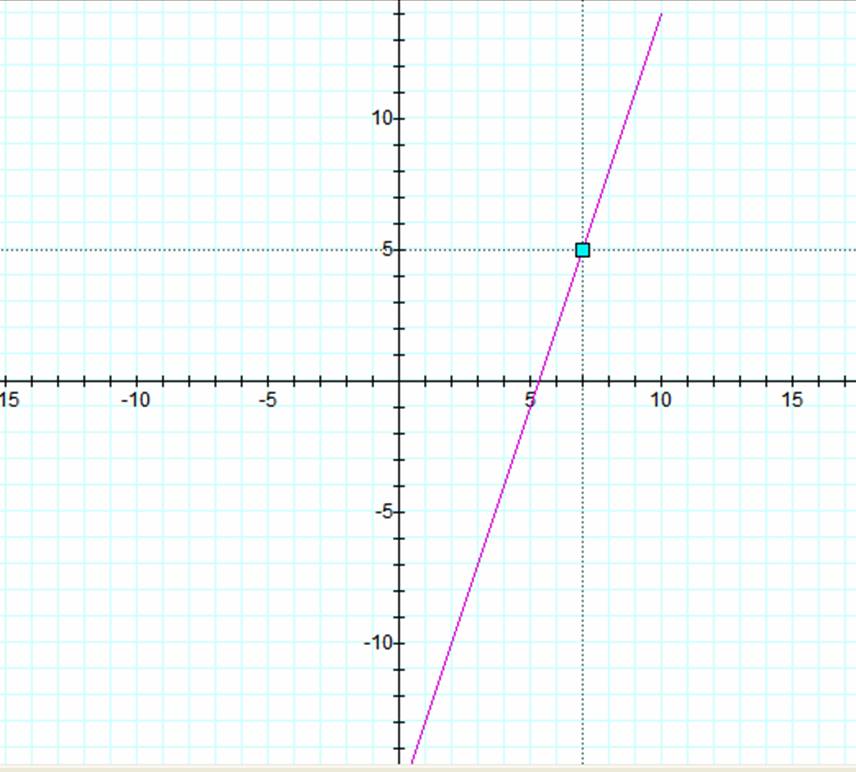
The blue point on the graph has approximately the following coordinates:

And t ranges from 0 to 10. In this case, the line extends more in either direction depending on how t is changed. If t goes up to 20, the length of the line segment will double. If t is changed to between -10 and 10, then the line segment will extend to the left the same length that it did to the right.

RETURN