Polar Equations
Assignment 11
Problem #1
By Erin Cain
In this problem we are asked
to investigate the following equation:
Let us begin by graphing the above equation. Note that in this equation, a, b, and k are held
constant or they are equal to one.
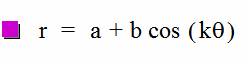
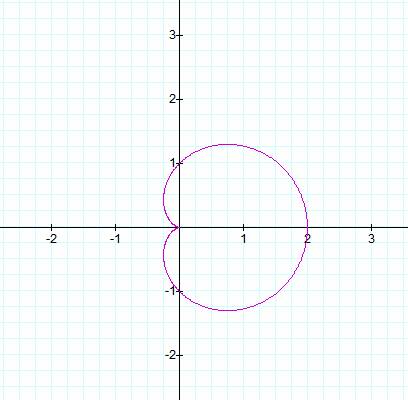
As you can see from above, in this case a, b,
and k are equal to 1. What will happen
to the graph if we keep a and b equal to 1, but vary k? What will we notice?
This time, let’s let k = 2 and see what
happens.
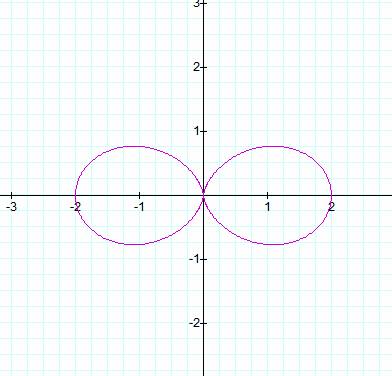
This time, when k = 2, we end up with 2,
leaf-like objects. Is this just a
coincidence or does the value of k, when a and b are 1, determine the number of
leaves we have? Let’s now see what
happens when k = 3.
So far, it seems true that k
determines the number of leaves we will have in our drawing. To be absolutely certain, let us check when k
= ½ and when k = 50.
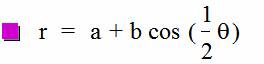
When we look at the case when
k = ½, we can see that the graph looks like it is approximately half of the
graph we got when k = 1. Then if you
look at the graph where k = 50, you will notice that there are 50 leaves in
that graph. Therefore, it is true that the
value of k when a and b are 1 tells us the number of leaves we will have in our
graph. Hence, when a and b are equal and
k is an integer, the equation gives
us what we call a “n-leaf rose”.
Let’s now move on and explore
the polar equation 
. Similar to what we did above, we will now see
what happens when we vary k but keep b equal to 1. We will start with the graph of the above
equation.
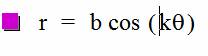
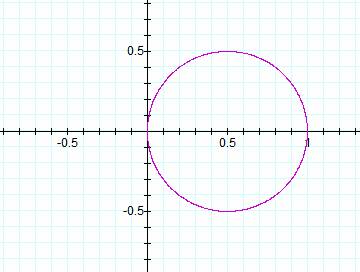
Looking at this graph, we could easily say that this
graph only has one leaf and k = 1 in the equation. Therefore we could hypothesis, as we did
before, that k determines the number of leaves you will have in your graph. In order to determine if this is true or not,
we need to explore some more.
In this case when k = 2, we do not get two
leaves. Instead, we find that our graph
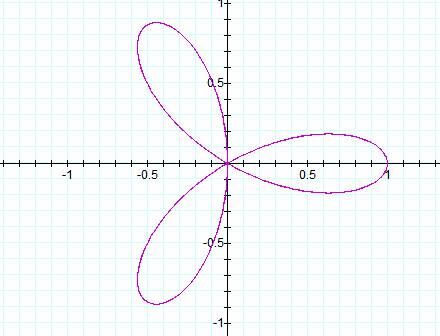
has 4 leaves. Let us now try it for when
k = 3 to see if we notice any common pattern among the equations and the
graphs.
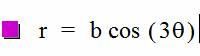
Now in this situation, k does determine the number of
leaves on the graph. Due to the fact
that when k was one and three, there were k number of leaves in the graph and
when k was two, there were 2k leaves on the graph. Therefore we can hypothesize that if k is an
odd number, then there will be k leaves on the tree. If k is an even number, then there will be 2k
leaves in the graph. We can do a couple
more examples to prove that this hypothesis is correct.
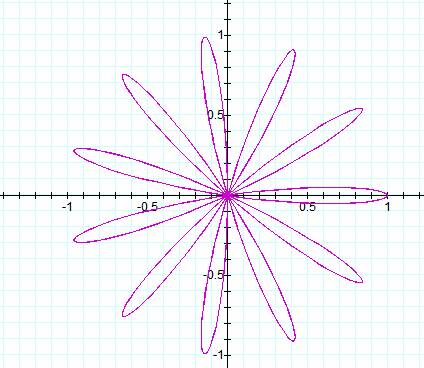
In the above examples, when k = 11, there were 11
leaves, and when k = 12, there were 24 leaves.
Therefore our hypothesis stands true; when k is an odd number, then
there are k leaves, but when k is an even number, then there are 2k leaves.
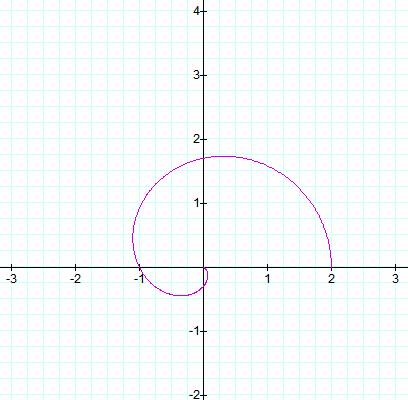
Now let us explore what will happen if we vary both b
and k at the same time. We will begin by
looking at 
. According to what we have learned so far,
there should 4 leaves in this graph.
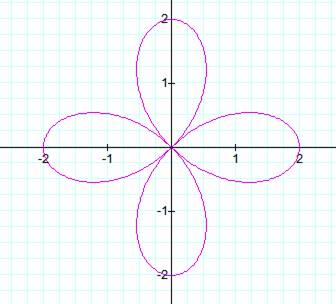
We were right with the number of petals, but now,
instead of the petals only extending to 1, they extend to 2 or -2 depending on
which axis you are on. Therefore, we can
hypothesis that nothing new will happen with k, if k is odd then there are k
leaves but if k is even then there are 2k leaves, and the value of b will
determine the length of the leaves. Let’s
look at k = 3.
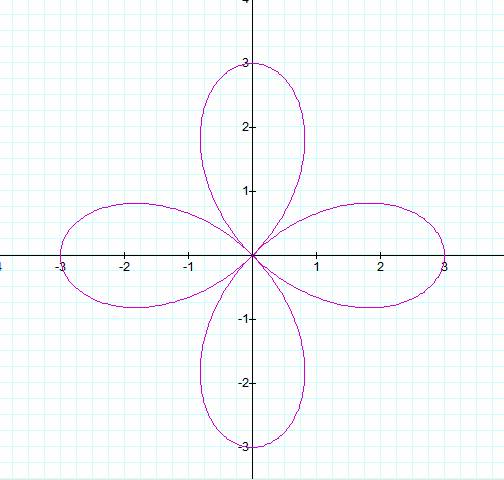
So far so good, our hypothesis seems to hold. Let us try one more example.
Here, we now have b = 4 and k = 3. We also have 3 leaves and leaves with a
length of 4. We can now assume that our
hypothesis is true: b is the length of the petals and if k is odd, then there
are k petals, and if k is even, then there are 2k petals.