
The Different Centers of a Triangle
Assignment 4
Problem #5
By Erin Cain
In this problem we are asked
the following:
Use GSP to construct G, H, C, and I for the same triangle.
What relationships can you find among G, H, C, and I or subsets of them?
Explore for many shapes of triangles.
To begin with, let’s clarify the labeling
used in this write-up.
G = Centroid; H = Orthocenter; C
= Circumcenter; and I = Incenter.
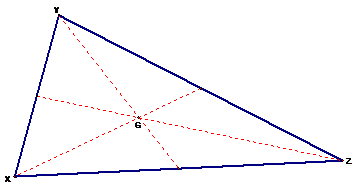
A triangle with all four
centers in it looks like the following:

To explore this on your own before reading on, you can
CLICK HERE to change the shape of the triangle and
see how the centers react.
Centroid (G):
The centroid of a triangle is
the common intersection of the three medians.
Note that a median is the segment that connects a vertex to the midpoint
of the opposite side.
The centroid is more often
than not referred to as the “center” of the triangle. It is not completely clear to say that it is
just the center of the triangle.
Instead, think of the centroid as the center of mass inside the
triangle. If you think of the triangle
as a 3D object, then you could balance it on your finger at the centroid. Therefore the centroid must always remain
inside the triangle.
Orthocenter (H)
The orthocenter is the common
intersection of the three lines containing the altitudes of the triangle. Note that an altitude is a perpendicular
segment from the vertex to the line of the opposite side.

The orthocenter can be inside or outside the triangle,
unlike the centroid. The only
restriction is that the orthocenter can only move outside the triangle by way
of a vertex. This is because in order to
construct the orthocenter, you must construct the altitude which is formed by
using the vertices of the triangle. The
orthocenter stays inside the triangle when the triangle is acute, and when the
triangle is obtuse, the orthocenter moves outside the triangle. You can explore this more on your own HERE.
Circumcenter (C)
The circumcenter is the point
in the plane that is equidistant to all three vertices. Since a point equidistant from two points
lies on the perpendicular bisector of the segment determined by the two points,
the circumcenter is on the perpendicular bisector of each side of the
triangle. In other words, the
circumcenter is the intersection point of the perpendicular bisectors of each
side.

The circumcenter is also the center
of the circumscribed circle, the circumcircle, or the triangle.

Similar to the orthocenter,
the circumcenter can be inside or outside the triangle. Same as the orthocenter, the circumcenter
moves outside the triangle when the triangle is obtuse and is inside the
triangle when the triangle is acute. The
circumcenter moves out of and into the triangle by way of the midpoint on each
side. You can explore this for yourself
by clicking HERE.
Furthermore, the circumcenter lies on the hypotenuse of a right
triangle.
Incenter (I)
The incenter is the point on
the interior of the triangle that is equidistant from the three sides. Since a
point interior to an angle that is equidistant from the two sides of the angle
lies on the angle bisector, then I must be on the angle bisector of each angle
of the triangle. In other words, the
incenter is the point of intersection of all three angle bisectors.

Due to the fact
that angle bisectors pass through the interior of a triangle, we know that the
incenter must always lie inside the triangle.
Similar to the circumcenter, the incenter is the center of the inscribed
circle, also known as the incircle.
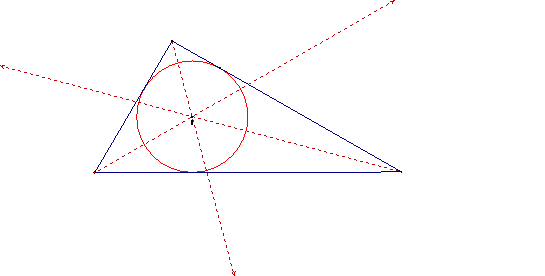
Observations:
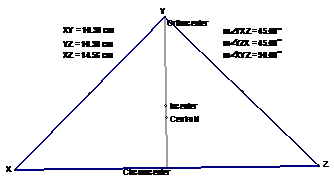
One of the most
interesting facts about the centers G, H, and C is that they all lie on one
straight line. To go along with that,
they also have the same ratio of the distance between them. The ratio of GC to HG is always equal to one
half. In other words, the distance from
the centroid to the orthocenter is always twice the distance from the centroid
to the circumcenter. You can explore
this for yourself by clicking HERE. Another observation that should be pointed
out is that these 4 centers become one center in an equilateral triangle.
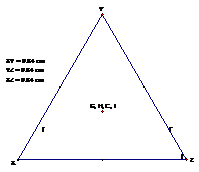
If the triangle
we are looking at is an isosceles triangle, all 4 of the centers line up on the
same line.
One last
observation made is that the area of triangle