Altitudes and Orthocenters

Assignment 8

Problem #1 - #7

By Erin Cain

In this problem, we are asked the following:

1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.

7. Conjectures? Proofs?

1) Construct any triangle ABC.

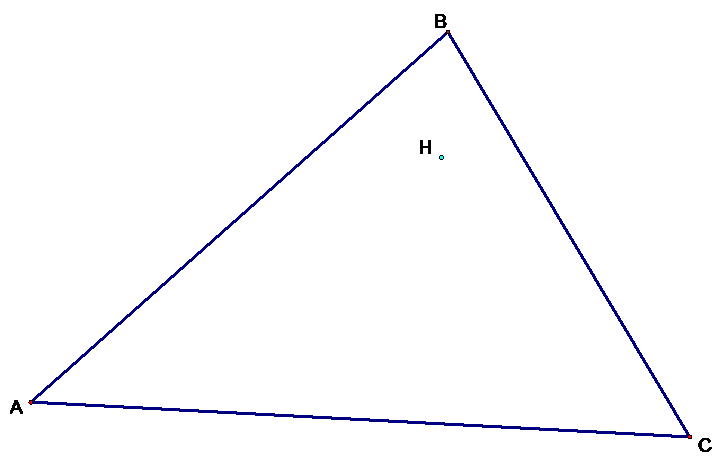
2) Construct the Orthocenter, H of the triangle.

3) Construct the orthocenter, X, of triangle HBC.

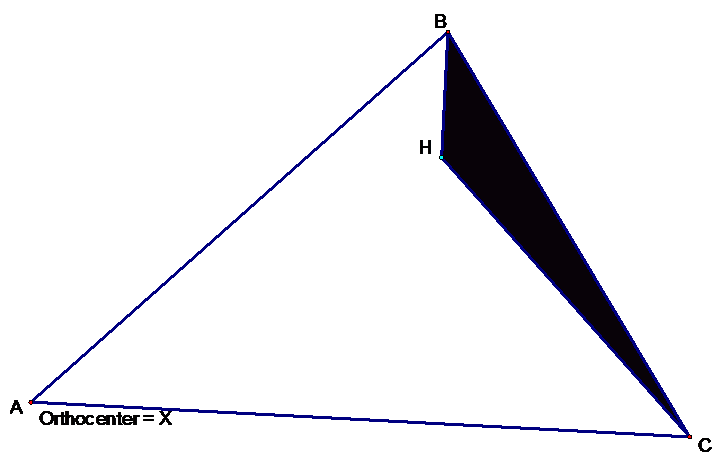
Notice here that the orthocenter is at the vertex opposite the side of the original triangle that is being used in HBC.

4) Construct the orthocenter, Y, of HAB.

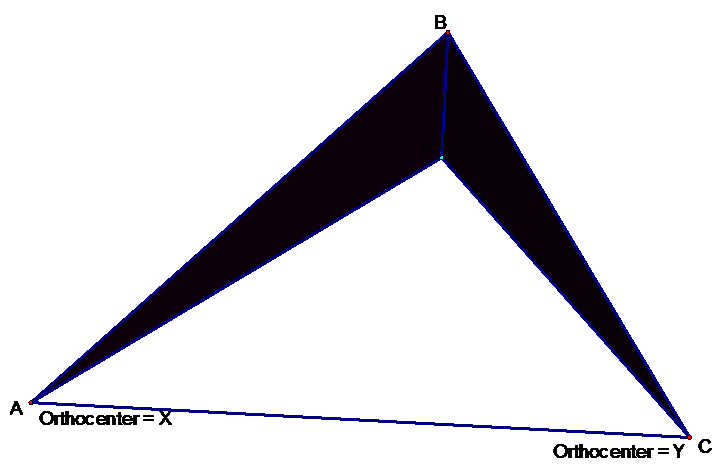
Once again, the orthocenter is at the opposite vertex.

5) Construct the orthocenter, Z, of HAC.

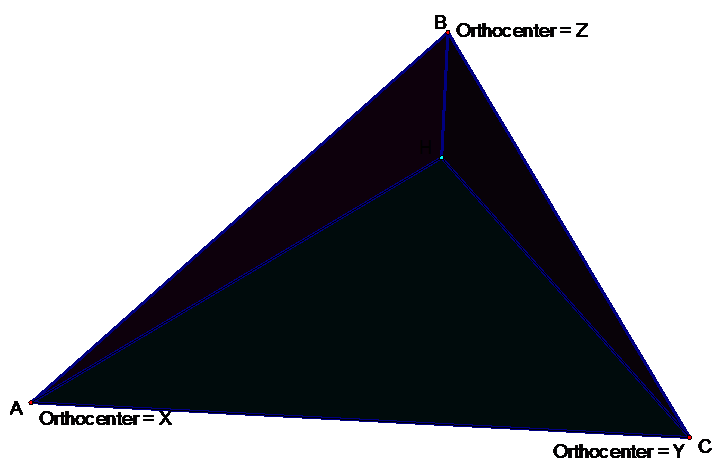
6) Construct the circumcircles of triangles ABC, HBC, HAB, and HAC.

In order to do this, we must first construct the circumcenter of each triangle. The circumcenter is the intersection point of the perpendicular bisectors of each side. Then to construct the circumcircle, we use the circumcenter as the center of the circle and one of the triangle’s vertices as a point on the circle. In the picture below, P, Q, R, and S are the circumcenters of the four different triangles and these circles are color coordinated with their triangle.

7. Conjectures?

Well, from looking at the above construction, I was unable to make any good observations besides that the orthocenters of triangles HBC, HAB, and HAC are at the vertices of the original triangle ABC. Therefore I decided to see what happens when we connect the three orthocenters, X, Y, and Z, with the circumcenters for the triangles HBC, HAB, and HAC.

From looking at this construction, we can see that we have a six-sided figure known as a hexagon. It also looks as if the side lengths of this hexagon might be equal in length. Therefore I used the measurement tools in GSP to see if this is true.

As you can see above, this is true. After I manipulated the construction, I found that this is always true. I wanted to see when I would find a regular hexagon, and I assumed it would be when we have an equilateral triangle. Therefore I went through the above constructions again with an equilateral triangle and saw the following:

Here you can see that when triangle ABC is an equilateral triangle, we will have a regular hexagon when we connect the orthocenters and circumcenters of the smaller three triangles. Also note that when our original triangle is equilateral, all of the circumcenters lie on the circumcircle for the original triangle, the orthocenter and circumcenter of the original triangle is the same point, and all three smaller triangles, HBC, HBA, and HAC, all have the same area.

RETURN