Exploration of Pedal Triangles

Assignment 9

Problem #9

By Erin Cain

In this problem we are asked the following:

Find all conditions in which the three vertices of the Pedal triangle are collinear (that is, it is a degenerate triangle). This line segment is called the Simson Line.

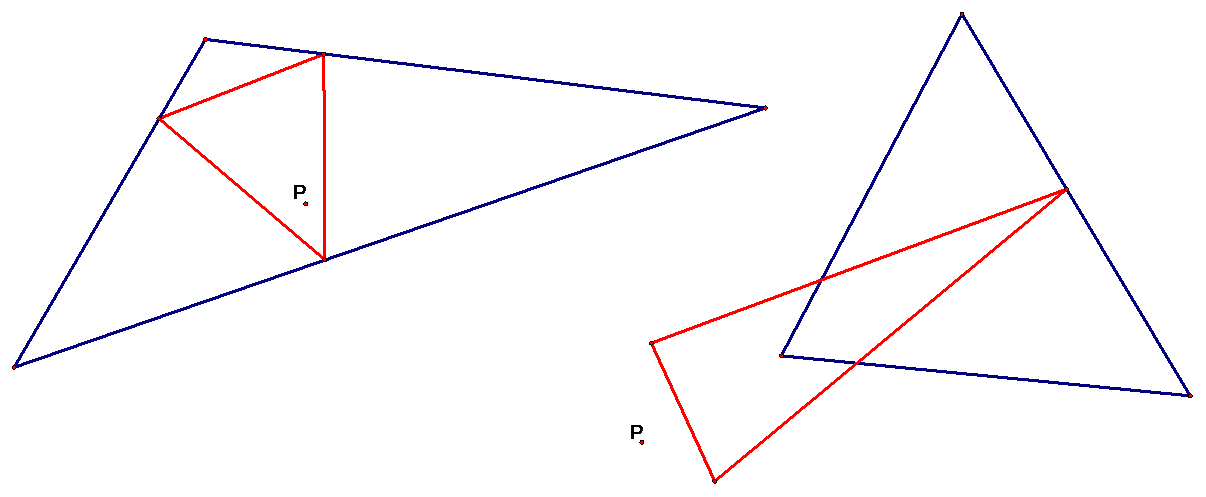
Let’s begin by developing an understanding of what a pedal triangle is. In order to construct a pedal triangle, we must first construct any triangle and then place a point P anywhere in the plane (either inside or outside of the triangle). You then construct lines that go through P and are perpendicular to each side of the triangle. Mark the intersections of the sides and then connect the three points using lines. This triangle is your pedal triangle. You need to note that when you are constructing this on GSP, you need to construct the original triangle and the pedal triangle using lines, not line segments, in order to see the pedal triangle in all cases. You can then hide the lines and reconnect the points by using line segments so that you can make your drawing neater. Here are some examples of pedal triangles for different locations of pedal point P.

A GSP script tool for this construction can be found HERE.

One type of pedal triangle is called the Simson Line. This occurs when the vertices of the pedal triangle are collinear (this is also referred to as the degenerate triangle). We will now explore pedal triangles by finding all cases where the Simson Line will occur.

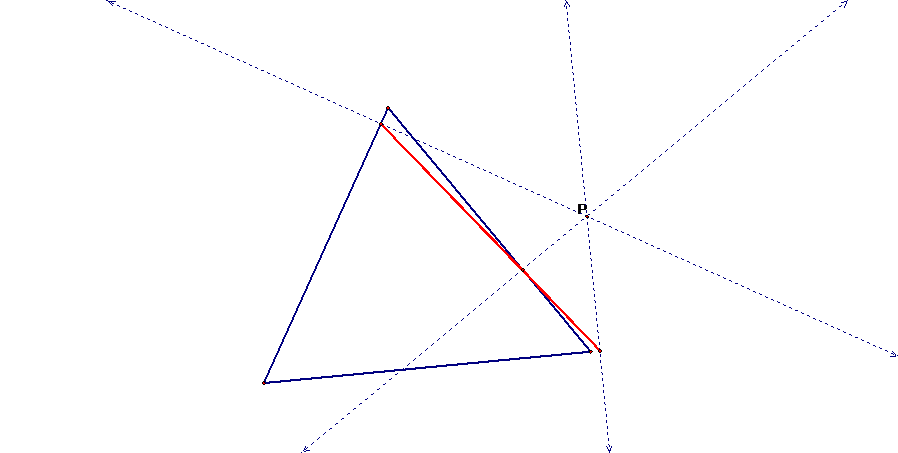
1) When P is one of the vertices of the original triangle.

Some would say that this case is obvious without any manipulation of the picture. If you remember the construction of the pedal triangle, it is formed by the vertices are formed by the lines that go through P and are perpendicular to each side. Therefore, if P is on one of the vertices of the original triangle, the intersection of the perpendicular line for that side and its adjacent side will be at the point as well. Therefore, you have two vertices of the pedal triangle at P, and that leaves one vertex of the pedal triangle. Hence, the Simson Line is a median (a line that is perpendicular to one side of a triangle and that goes through the opposite vertex) of our original triangle when P is on one of the three vertices.

2) By moving P around the plane, I found a few more places where we had a Simson Line. Some examples are below.

From moving P about the plane, I was noticing somewhat of a circular pattern when finding points where the vertices of the pedal triangle were collinear. You by using the tracing tool on GSP I was able to notate some of my observations, which can be seen below.

As you can see from my above exploration, it looks as if the vertices of the original triangle lie on a circle. From this I decided to construct the circumcircle of our original triangle. When I move P along this circle, the three vertices of the pedal triangle remain collinear. Therefore, all three vertices of the pedal triangle are collinear when P is on the circumcircle.

To see an animation of this in GSP, click HERE.

RETURN