Bouncing Barney

Final Assignment

Part A

By Erin Cain

In this problem we are asked to explore the following:

Barney is in a triangular room. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.

Let’s begin by constructing Barney’s path. I picked an arbitrary point on BC for Barney to start his journey. He then walks from this point, on a path that is parallel to AC, to AB.

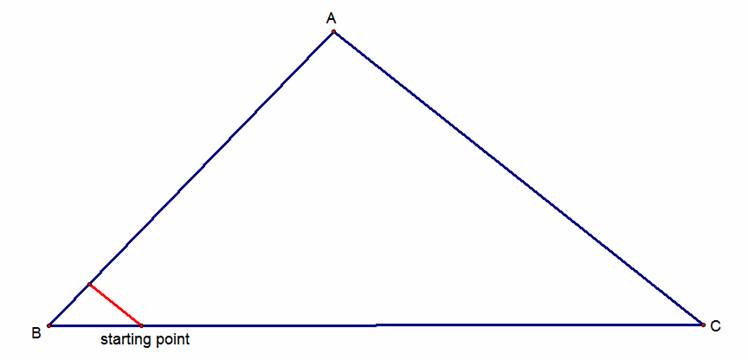
Once he reached AB, he turned and walked parallel to BC until he reached AC.

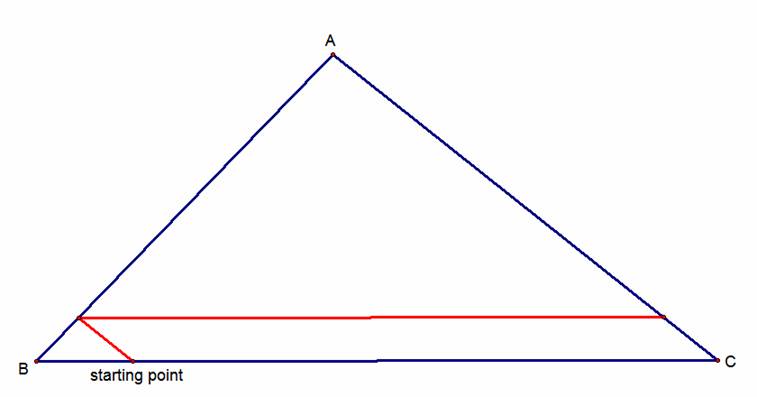
Once he reaches AC, he then turns and walks parallel to AB until he reaches BC.

In the problem we are asked to determine whether or not Barney will ever return to his starting point, and if so, then after how many bounces. In order to do this, we must continue constructing paths according to the pattern for Barney to walk on. Therefore, once he returns to BC, he once again turns and walks parallel to AC until he reaches AB.

Similar to before, once he reaches AB, he turns and walks parallel to BC until he reaches AC.

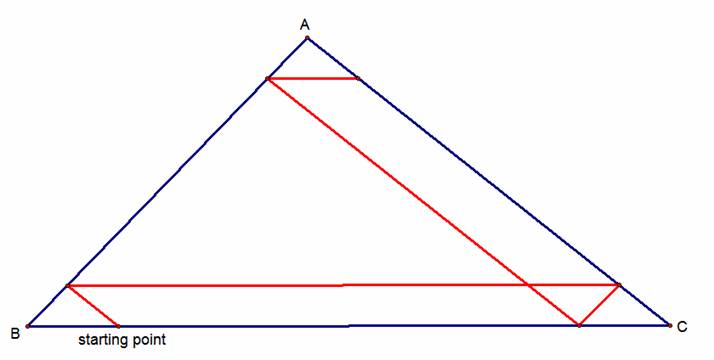
Now he turns and walks parallel to AB until he reaches BC.

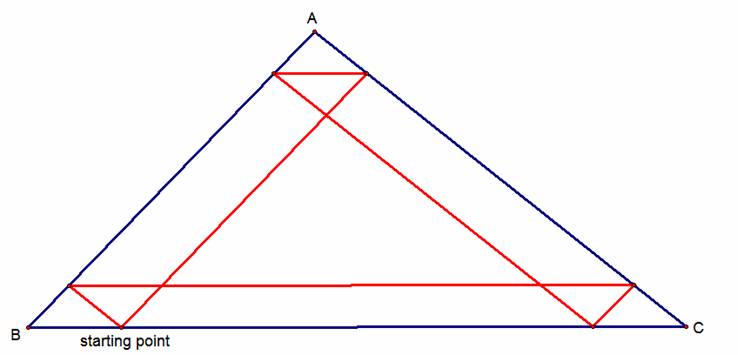
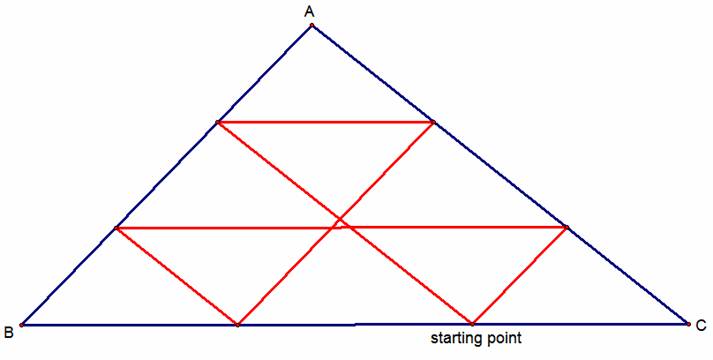
As we can see from the above picture, Barney does return to his starting point, and in the case above, it was at the 6 bounce. Let’s see what happens when we change the position of the starting point.

Once again we have the same result, Barney returns to his starting point at the sixth bounce. What will happen when Barney starts at the midpoint of BC?

As you can see from the picture, when Barney starts at the midpoint of BC, he returns to the starting point at his third bounce. Therefore it took half as many bounces in this case. This will also happen when the starting point is at one of the vertices of triangle ABC. What will happen when Barney starts outside of the triangle, but still on the same line as BC?

In this situation, Barney still returns to his starting point on his 6^th bounce, but the difference is that the bounces are off of the outside of the triangle.

Now that we have seen that Barney will always return to his starting point, we need to prove why this happens. Let’s begin our proof by referring to the following diagram.

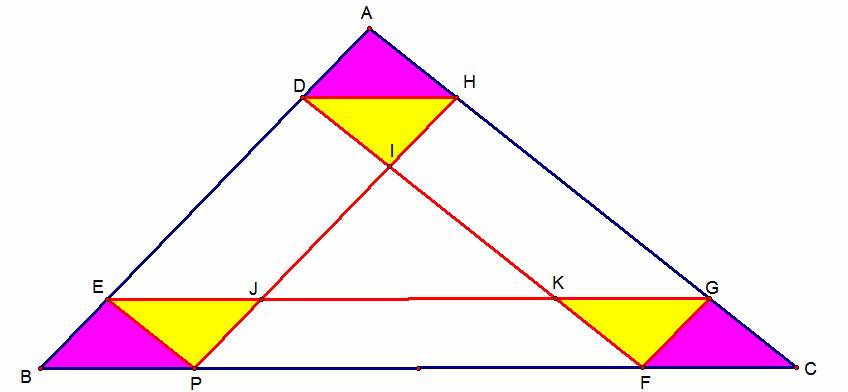
First note that I picked an arbitrary point P to be Barney’s starting point. The first thing I noticed in the construction of Barney’s path was that it formed many parallelograms and triangles. Therefore I will prove that Barney will always end up at his starting point using what I know about parallel lines, transversals, angles, parallelograms, similar/congruent triangles, proportionality, and transitivity.

Let’s identify the lines that are parallel in our construction; there are three sets of them. The first set of parallel lines contains AC, DF, and EP. The next set contains AB, HP, and FG. Our final set of parallel lines contains BC, EG, and DH. The parallel line/transversal theorem states the following: If two or more parallel lines are cut by a transversal, then the corresponding angles are congruent. All of our sets of parallel lines are being cut by transversals; therefore we know that we will have some congruent angles. The sets of congruent angles are:

Angles ABC, ADH, HJG, HPC, DEG, and GFC are congruent

Angles DAH, BEP, PIC, FGC, PHC, and EDK are congruent

Angles ACB, AGE, AHD, IKJ, EPB, and IFP are congruent

Now that we know our congruent angles, we can find similar triangles by the Angle – Angle (AA) Theorem. Therefore, by AA, the following triangles are similar:

Triangles ABC, AEG, ADH, HJG, HPC, GFC, and EBP

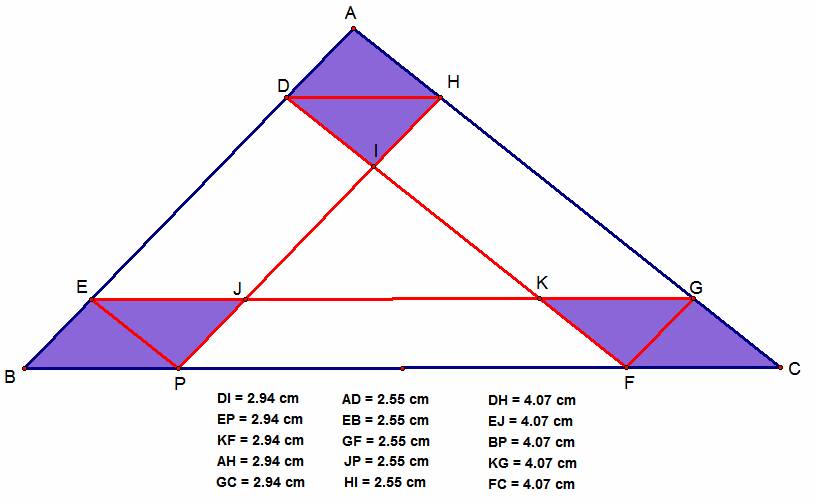
The two pink triangles in the picture above are similar and they are both adjacent to a yellow triangle. The pink triangle combined with the yellow triangle forms a parallelogram due to the fact that the lines EG and BC are parallel to each other by construction and the line segment EJ and KG lie on the line segment EG, and then BP and FC lie on the line segment BC, hence making these parallelograms. We now need to show that these parallelograms are actually congruent to each other. In order to do this, we must show that the diagonal of these parallelograms cuts the parallelogram into two congruent triangles. We know that triangle BEP is congruent to JEP, triangle FGC is congruent with KFG, and that triangle ADH is congruent with IDH. Therefore, by the transitivity property, we know that all of the colored triangles are congruent to each other. Therefore, in the picture below, the purple parallelograms are congruent to each other.

Now we can use what we have found out above to finish the proof. First off, if Barney does not return to his starting point, P, then, after his 5^th bounce, he must hit at some random point on BC. Let’s mark this point in our construction as point X.

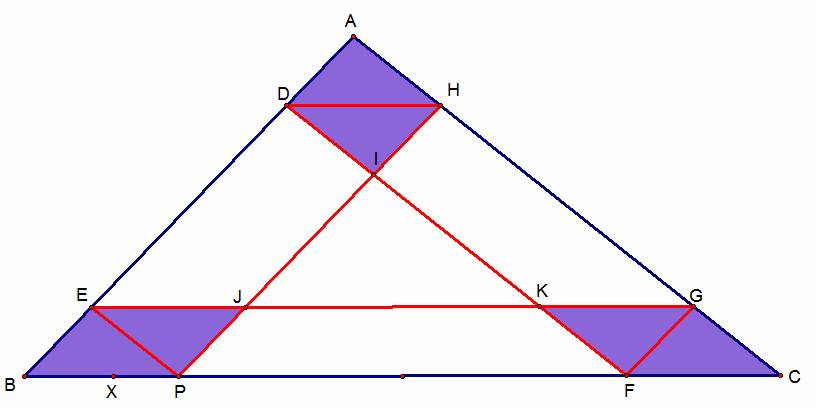
We can now use our knowledge of proportionality to come up with the following equation:

AH/AC = AD/AB = FC/BC

We using this same idea, we can write BX/BC = AH/AC. By the transitivity property, we can now write the following:

BX/BC = AH/AC = AD/AB = FC/BC

BX/BC = FC/BC

Since BX/BC is equal to FC/BC, then BX must equal FC. Due to the fact that triangle FGC is congruent to triangle BEP, BX = BP, therefore the point that Barney must hit after his 5^th bounce (i.e. at the 6^th bounce), X, must be point P. Therefore X = P, hence Barney will always return to his starting point.

QED.