
Spreadsheet Math
Exploration
by
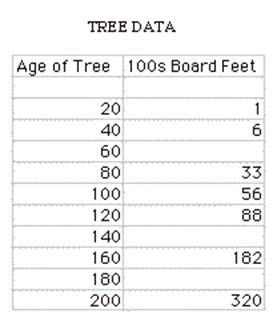
Exploration: This data is from the lumber industry,
giving the approximate number of board feet of lumber per tree in a forest of a
given age. What function will fit the data? Predict the harvest for ages other
than those given.
Before I start
modeling, is there a way of knowing when you found a good model? One measure of how well the model fits
the data is the correlation coefficient, but this applies only to linear
models. Another way to decide how
well a model fits a data set is to examine the errors. Error = observed y – predicted y, often
called the residual in statistics.
A scatterplot of the residuals to the value of
the independent variable helps determine whether a proposed model is a good
fit. If the model is a good fit,
the residuals should tend to fall within a horizontal band centered around zero.
Residual Plot: Good Fit
Residual Plot: Better Fit Available
Residual Plot: Better Fit Available
So, before we begin,
let us look at a graph of the tree data.
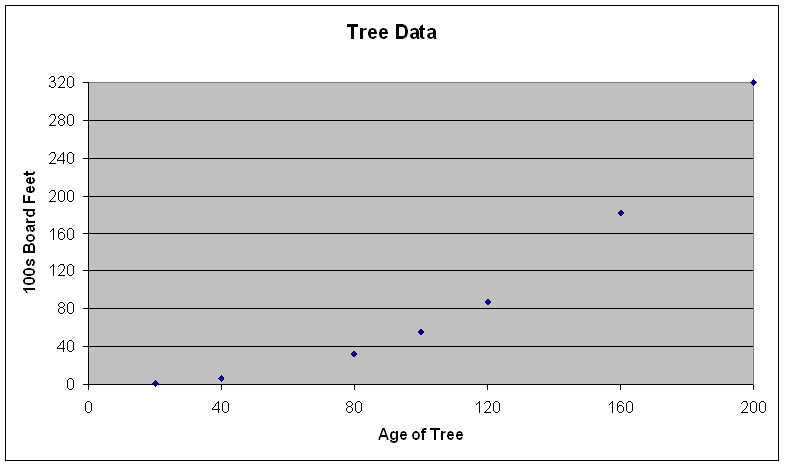
Looking at the graph,
it appears the model may be exponential or some polynomial with degree higher
than 1 (like quadratic or cubic).
Now, we are going to use a TI-84 to explore different possibilities for
the model, and we will look at the residual plot to determine if a better model
exists.
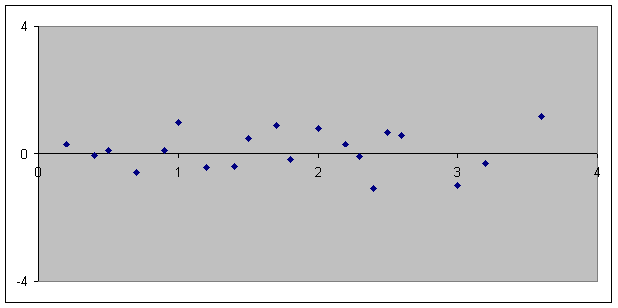
Linear Model: y = 1.7097x – 77.8592
|
Age
of Tree |
100s
Board Feet |
Linear
y(age) |
Residuals |
|
20 |
1 |
-43.6652 |
44.6652 |
|
40 |
6 |
-9.4712 |
15.4712 |
|
80 |
33 |
58.9168 |
-25.9168 |
|
100 |
56 |
93.1108 |
-37.1108 |
|
120 |
88 |
127.3048 |
-39.3048 |
|
160 |
182 |
195.6928 |
-13.6928 |
|
200 |
320 |
264.0808 |
55.9192 |
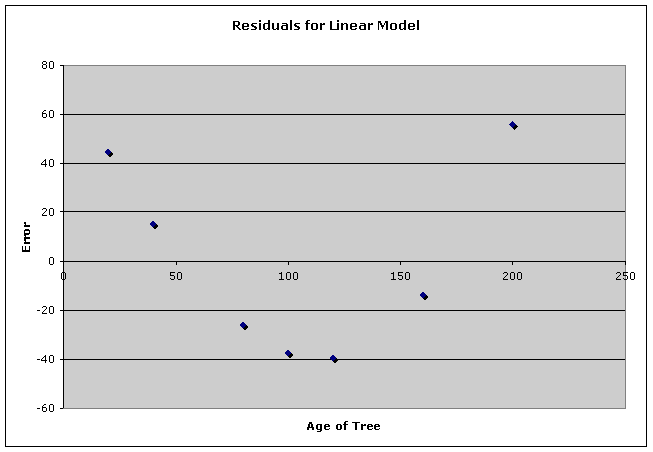
According to the residual plot for
the linear model, a better model exists.
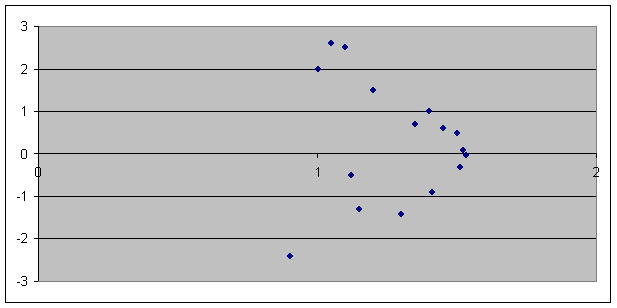
Quadratic
Model: y = 0.0110x2
– 0.6812x + 13.3131
|
Age
of Tree |
100s
Board Feet |
Quadratic |
Residuals |
|
20 |
1 |
4.0891 |
-3.0891 |
|
40 |
6 |
3.6651 |
2.3349 |
|
80 |
33 |
29.2171 |
3.7829 |
|
100 |
56 |
55.1931 |
0.8069 |
|
120 |
88 |
89.9691 |
-1.9691 |
|
160 |
182 |
185.9211 |
-3.9211 |
|
200 |
320 |
317.0731 |
2.9269 |
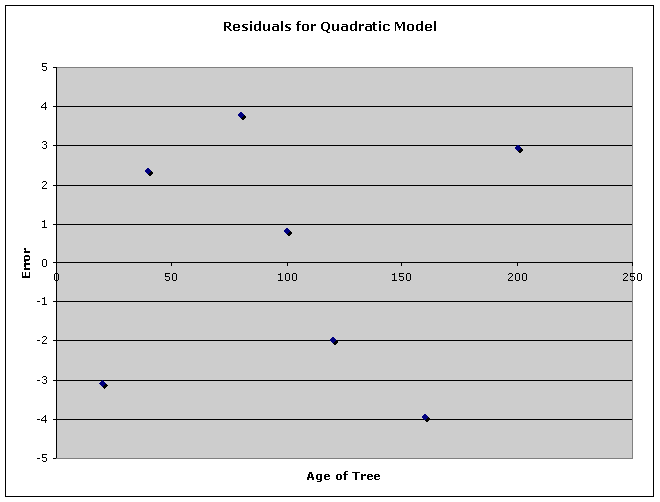
According to the residuals for the quadratic model,
this model is a good fit. However,
let us continue our exploration and see if the errors can decrease.
Cubic Model: y = 2.0983E-5x3 + 0.0041x2
– 0.06251x + 0.5298
|
Age
of Tree |
100s
Board Feet |
Cubic |
Residuals |
|
20 |
1 |
1.087464 |
-0.087464 |
|
40 |
6 |
5.932312 |
0.067688 |
|
80 |
33 |
32.512296 |
0.487704 |
|
100 |
56 |
56.2618 |
-0.2618 |
|
120 |
88 |
88.327224 |
-0.327224 |
|
160 |
182 |
181.434568 |
0.565432 |
|
200 |
320 |
319.8918 |
0.1082 |
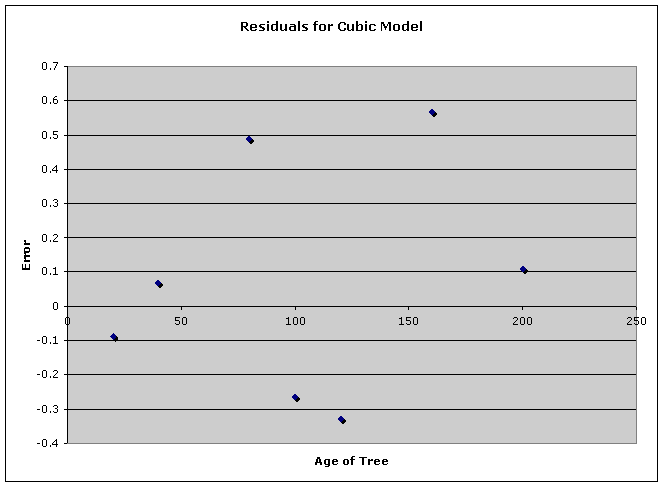
This residual plot is
considerably better. Notice in the
quadratic model, one residual is -3.92. In the above residual plot for the cubic
model, the largest residual is 0.57 (closer to having no error). So far this is the best model.
Quartic Model: y = -3.3659E-8x4
+ 3.5890E-5x3 + 0.0019x2 + 0.0584x - 1.3251
|
Age
of Tree |
100s
Board Feet |
Quartic |
Residuals |
|
20 |
1 |
0.88463456 |
0.11536544 |
|
40 |
6 |
6.26169296 |
-0.26169296 |
|
80 |
33 |
32.50390736 |
0.49609264 |
|
100 |
56 |
56.039 |
-0.039 |
|
120 |
88 |
88.08128976 |
-0.08128976 |
|
160 |
182 |
181.6055778 |
0.39442224 |
|
200 |
320 |
319.6205 |
0.3795 |
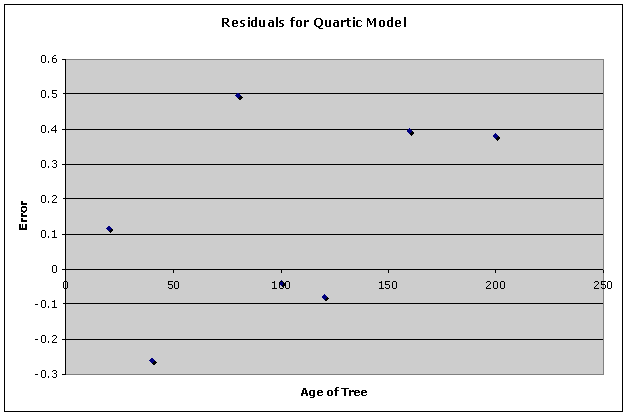
Now, the quartic
model is the best fit for the tree data. Notice the largest residual is 0.496
rather than the 0.57 residual in the cubic model.
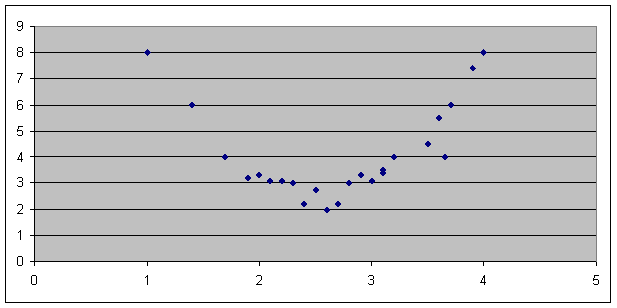
Exponential
Model: y = 1.5703*1.0305x
|
Age
of Tree |
100s
Board Feet |
Exp |
Residuals |
|
20 |
1 |
2.863799131 |
-1.86379913 |
|
40 |
6 |
5.222788934 |
0.777211066 |
|
80 |
33 |
17.37089999 |
15.62910001 |
|
100 |
56 |
31.67978622 |
24.32021378 |
|
120 |
88 |
57.77529405 |
30.22470595 |
|
160 |
182 |
192.159566 |
-10.159566 |
|
200 |
320 |
639.1191841 |
-319.119184 |
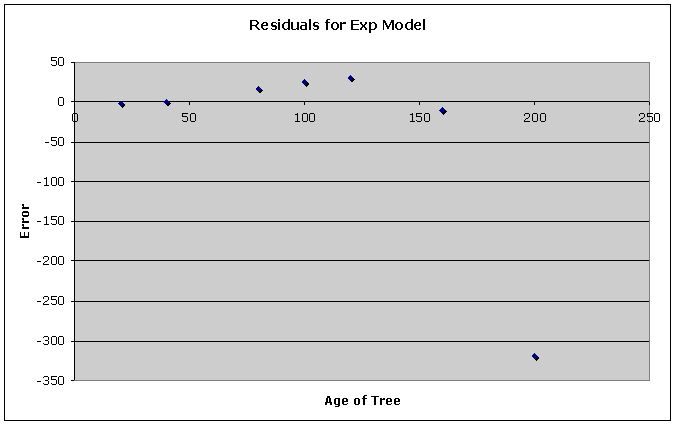
Notice a problem. One residual is -319.119. This model is not acceptable.
Conclusion: What’s the best fit? According to the residual plots, the quartic model is the best fit. However, the tree data is dealing with
volume of useable lumber. Thus, the
cubic model fits the data well.
Cubic Model: y = 2.0983E-5x3
+ 0.0041x2 – 0.06251x + 0.5298