A Review of Basic Probability: Days 1-2 (or 3)

We’ve all heard of probability in some shape or form. This is especially true in election years!

So what, in its basic form, is probability? What does probability mean?

In basic terms, probability is the likelihood that some event will happen over extended periods of time.

For example, in a standard deck of playing cards (52 total cards), what is the likelihood (or probability) that you will choose an Ace just by choosing one card at random?

Notice the color scheme above. You see, when determining probability, we are always concerned with some particular “event” of interest. In the above example, “choosing a Queen card” would also be an event, but would not be the particular “event” of interest in the above example.

When determining basic probability, we need to determine the “sample space” and identify the number of “favorable events.”

The sample space consists of all the possible outcomes that could take place. So in the example of the deck of cards, the sample space would be 52. What would you think “favorable events” would be for the above example?

So if you pull a card from the deck, we call that a trial. In simple terms a trial could be considered any of the following:

· Choosing a card from a deck of cards

· Rolling a number cube

· Pulling a piece of clothing out of your clothes drawer

· Flipping a coin

· Testing a patient in a clinic to see whether or not a new drug is effective

· (Perhaps you get the idea)

There is another key idea we’ve touched on earlier: the idea of randomness. For example, if you choose a card at random from a 52-card deck, then you have no idea which card you are going to choose. So the idea of randomness implies that the outcome of the trial is unknown prior to the trial.

Activity: If you roll a die (or number cube), what is the probability of obtaining a 1? We’ll use the built-in feature of the TI-84 “Simulation” Application to determine the long-term results for rolling a die. We will keep a count of the number of times we see a 1 appear on the number cube.

In a moment, you will complete a table like the one below. Let’s suppose that we roll a number cube 5 times and get the following numbers on the cube after each trial: 1, 3, 3, 1, 5

We would complete the table as follows:

Trial	1 Occurs? (yes/no)	Cumulative Proportion of 1’s	Simplified
1	Yes	1/1	1.0
2	No	1/2	0.50
3	No	1/3	0.3333
4	Yes	2/4	0.50
5	No	2/5	0.20

In other words, keep a running total of each one you see. After each trial, divide the number of ones you’ve seen up to and including that trial and divide by the number of trials you’ve performed so far. In the simulation above, we performed 5 trials and had a one appear twice, so our very last cumulative proportion is 2/5.

The question remains as to what happens as the trials continue long-term.

Follow the directions below and complete Table 1.1:

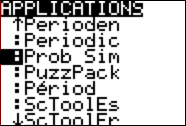
**On your TI-84, choose the APPS menu:

Choose “Prob Sim” from the menu:

Then press any key. If you cannot find “any key,” then the ENTER button will suffice.

Choose 2, “Roll Dice”.

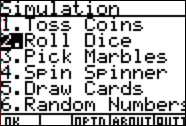
Follow the instructions on the calculator to count the number of times a 1 is rolled.

Trial	1 Occurs? (yes/no)	Cumulative Proportion of 1’s
1	/1
2	/2
3	/3
4	/4
5	/5
6	/6
7	/7
8	/8
9	/9
10	/10
11	/11
12	/12
13	/13
14	/14

Table 1.1

Questions for discussion:

1. In the “long run” (if you continue the experiment over long periods of time), what number does the “Cumulative Proportion of 1’s” approach? What if you continue to roll 50 times instead of 14?

2. If you roll a 2 on your first roll, does this determine whether or not you will roll a 2 on the second roll? (This is the idea of “independence”. In other words, an event is considered independent if one particular trial does not affect the next trial. In the example of rolling a die, the result of the first roll will not affect the result of the second roll.

3. What is the overall probability of rolling a tree on one die with one roll?

4. The Compliment of an event is defined as all of the other events in the sample space that are NOT the event A itself. The compliment of A is itself also a probability. How would you interpret the idea of the “Compliment of rolling a 1”?

5. How would the probability change if we were allowed to count a 1 or a 2 instead of just the number 1?

Investigation Two: Passing a True/False Quiz

Suppose you were given a five-question True/False quiz, but you forgot to study the night before. You decide, “Hey, I have a 50/50 chance of getting each question correct.” What does this mean about your chances of passing the quiz with a perfect score?

How many possible ways are there to answer a five-question true/false quiz? Let’s create a tree diagram to illustrate the possibilities after you’ve answered three questions:

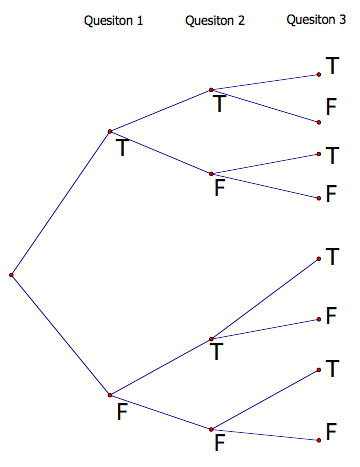
Discussion:

How many possibilities are there after you’ve answered three questions? Or, to put it another way, how many different ways could someone possibly answer three questions? (Hint: how many “points” are there under the Question 3 column?)

Can you determine how many ways someone could answer 5 questions on a true/false test? (Extend the chart if necessary).

If someone were to randomly guess at each question, what is the probability that this person will make a perfect score?

Simulation-Extension: Getting a Perfect Score on a Multiple Choice Test By Guessing Alone

Materials needed:

*A Partner

*A TI83+ or TI84 Calculator (or some other random number generator)

Person A will take on the role of the “teacher” and will create a 20-question, multiple-choice (four options) quiz. Using the TI84 calculator follow the steps below:

From the MATH button, choose PRB and select option 5:

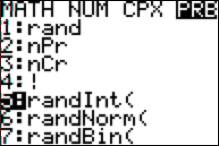
We wish to generate 20 different answers. For the sake of simplicity, we’ll generate answers one at a time. We will call each answer “1, 2, 3, or 4” (just as we would see answers a, b, c, or d on a multiple-choice test). Enter “1,4” into the calculator as follows. The calculator will now generate a random answer, either 1, 2, 3, or 4. Each time you press ENTER, it will generate another answer for you as the teacher.

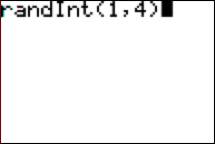
Person A should perform this calculation by recording the correct answers to the quiz in the middle column. Continue to press ENTER to generate more random numbers, 1-4. After recording the answers, have your partner guess each answer to each question without looking. Record his/her answers in the third column and calculate the score.

Question #	“Correct” Answer (from the calculator)	Person B’s answers (by guessing)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Can you extend your ideas from the true/false quiz to this more extensive quiz?

1. Explain how the tree diagram would look different after two questions.

2. Explain how the tree diagram would look different after five questions.

3. How big is the sample space of possible ways to answer the quiz (with all 20 questions)?

4. Find the probability of obtaining a perfect score on this quiz by guessing alone.

5. Interpret the idea of “Compliment” of the probability of obtaining a perfect score.

Summarize what you’ve learned: Create one sentence according to the following conditions:

1. Use as many of these words as possible: Probability, Trial, Randomness (or Random), Independence (or Independent), Sample Space, Event, Compliment, Tree Diagram, AND

2. Your sentence must make grammatical and logical sense.

Teacher Option: Discuss Venn Diagrams.

A web applet is available from the following site, which deals with Venn Diagrams and Probability:

http://stat-www.berkeley.edu/~stark/Java/Html/Venn3.htm

**Click Here for help from TI concerning the use of the Probability Simulation APP for the TI84