EMAT 6680 :: Clay Kitchings :: Assignment 8

Given triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully. Prove:

Part 1:

Part 2:

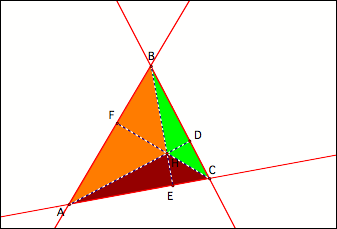
Part 1: Let us first set out to investigate how the ratios could possible sum to 1 in the first case.

To begin, we will see if we can find a convenient way to write these ratios in some other form, preferably a form that has common denominators.

I have color-coded smaller triangle within triangle ABC in order to help illustrate the method behind the “madness.” We shall consider the ratio of the areas of all the three colored triangles in relation to the area of triangle ABC.

Consider the following ratios :

**

Notice that I did not use the same expression for the area of triangle ABC each time. For the area of (ABC) we have some options to use. It was convenient for each denominator in each ratio to have an expression for the area of (ABC) such that one of the factors would divide out with a factor in the numerator.

Now, let us consider the sum of the following ratios:

(Common denominators)

Now, the sum of the three smaller (colored) triangles in the numerator sum to the entire area (ABC). Therefore we can substitute our ratios we found earlier into the equation above:

by substitution ** from above.

Part 1: QED

We want to verify that:

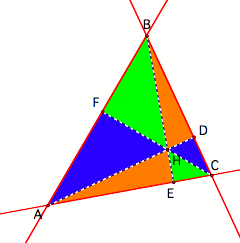
Let us rewrite the numerators knowing the following:

HD = AD – AH, HE = BE – BH, and HF = CF – CH

(The above is allowed due to basic segment addition and subtraction.)

We will replace the numerators in the previous proof with the expressions for HD, HE, and HF above and simplify to derive the proof:

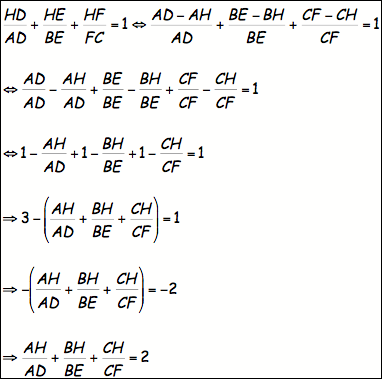
QED