EMAT 6680 :: Clay Kitchings :: Assignment 9 :: Pedal Triangles

Problem 9: Find all conditions for which the vertices of the pedal triangle are collinear (that is, a degenerate triangle). Note: This line segment is called the Simson Line.

How do you construct the Pedal Triangle?

It is obviously important to first know how to construct a Pedal Triangle if we are to investigate all conditions for which the vertices of the pedal triangle are collinear.

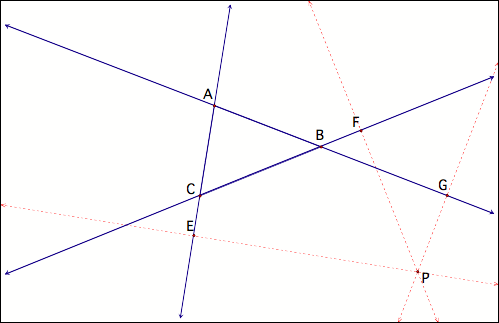
First, construct a triangle ABC. It is helpful to construct lines rather than segments. Construct any point P anywhere in the plane. Then construct perpendicular lines through P to Lines AC, AB, and BC. Below is a representative figure:

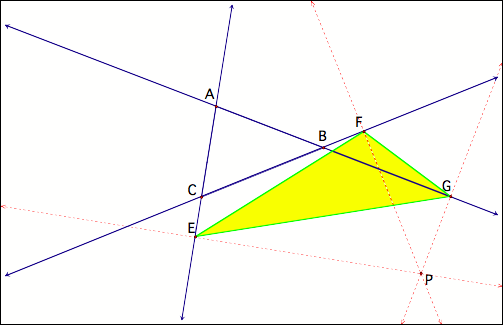
The Pedal Triangle is formed by the intersections of the perpendiculars to the lines AC, AB, and BC. The triangle (EFG) in yellow below represents the Pedal Triangle.

Now that we understand how to construct a Pedal Triangle, let us investigate cases for which the Pedal Triangle degenerates into a line segment. For a GSP File, click here.

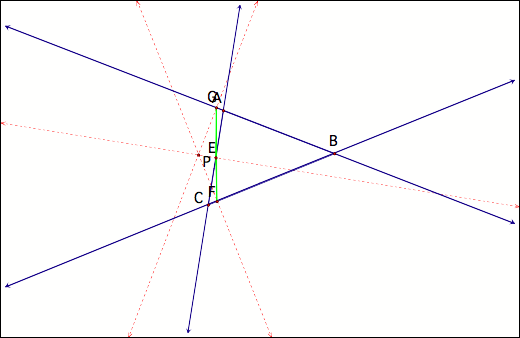
At first glance, we can visually conjecture that when the Pedal Point (P) lies on any vertex of triangle ABC, then triangle EFG degenerates into a segment. However, this seems to be more of a “special” case. It appears in this case that two vertices of the pedal triangle converge and become the same point. Are there other occasions for which the vertices of the pedal triangle are collinear and even perhaps distinct points? I found one approximate case within about 15-20 seconds by moving P about the plane to obtain the following figure:

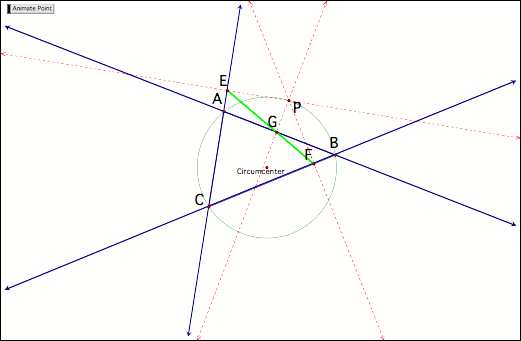
We can see that points E, F, and G are approximately collinear, and it is reasonable to assume (while exploring) collinearity near this region. Further movement of P about the plane could lead one to suspect some sort of circular pattern P such that if P travels this path, points E, F, and G are collinear.

I decided to construct the circumcircle of triangle ABC. Then, I used GSP’s “merge” tool to merge point P onto the circumcircle. I then animated P so that it would travel the path of the circle. Sure enough, points E, F, and G are collinear here.