EMAT 6680 :: Clay Kitchings :: Cycloids and Parametric Equations :: Assignment 10, Problem 12

A cycloid is the locus of a point on a circle that rolls along a line. Write parametric equations for the cycloid and graph it. Consider also a GSP construction of the cycloid.

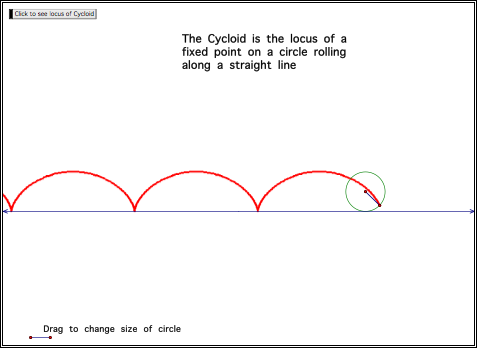
Our task is to come up with a parametric equation (or equations) to plot a cycloid.

My first inclination was to consider a situation such as |sin t|. So, I tried the following parametric and got the corresponding graph:

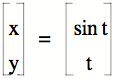
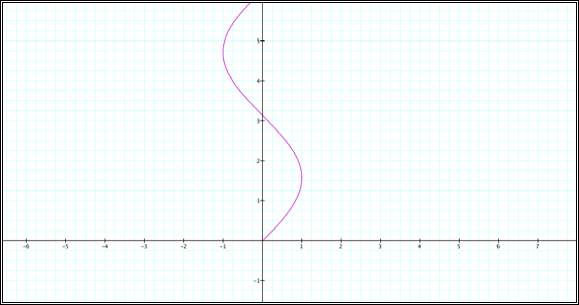
Obviously I wasn’t “fishing in the right hole.” I knew at once that my t needed to be in the x-row and the other function (presumably a trig function of some type) needs to be in the y-row.

I tried the following:

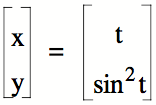
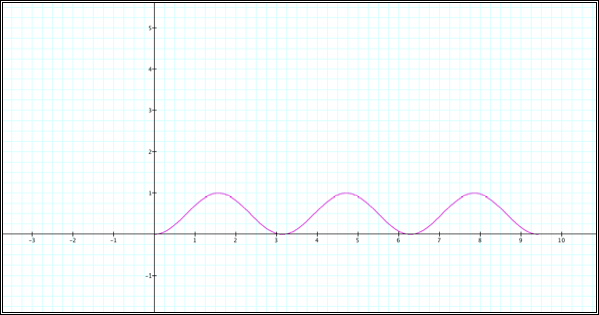
Now, I’ve managed to do… not very much! I need to somehow find the absolute value here to try to make the function become more of the cycloid path. However, Graphing Calculator does not have an absolute value function built in the program.

Therefore, I decided to “settle” for taking the square root as follows:

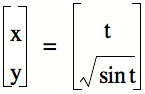
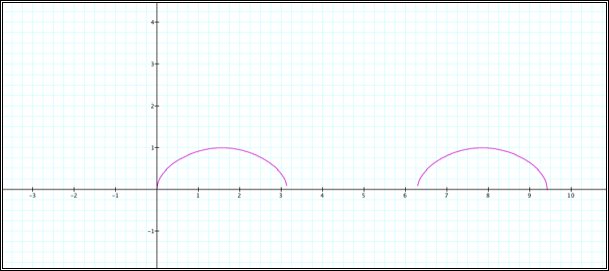
The “holes” in the graph are not surprising since the sine function yields negative values on [, 2], and the square root function is not defined for negative values. Therefore, the graph isn’t defined on those particular intervals.

My next idea was to create another parametric equation and translate the graph by a factor of .

The following screen capture displays the results:

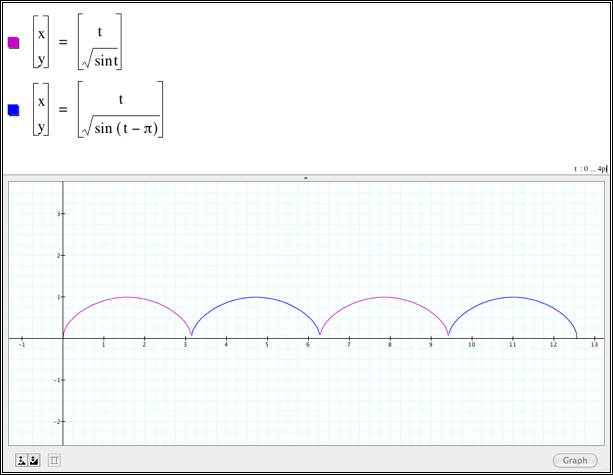
Now we are getting quite close to the cycloid graph. However, I would like to make this graph using one equation instead of two. I decided to revert back to my absolute value idea. Squaring the sine function and then taking an additional square root produces something that resembles an absolute value situation:

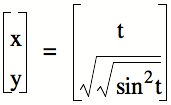
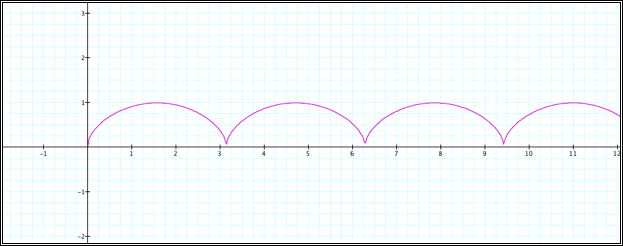
This parametric equation represents a cycloid such as is shown in the GSP file at the beginning of this assignment.