Clay Kitchings :: EMAT 6600 :: Rational or Irrational?

This problem was also inspired from MATH 6000 at UGA in the same semester I took EMAT 6600. Most of us (mathematics educators and mathematicians) have proved that is irrational. This problem is on the EMAT 6600 website of problems.

However, I wondered whether the same pattern (or shell of a proof) could be followed for numbers other than in order to verify that they are irrational. After seeing a proof for , I conjectured that all primes could be proven irrational similarly.

Problem: Show that is irrational for any prime number p.

We shall prove it is irrational by contradiction. So, let’s suppose that is rational and that it can be written as (We insert the relatively prime requirement to basically say we can write the rational number in lowest terms.)

This implies:

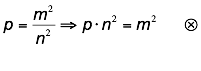
It is worth noting that other irrational numbers may be proven irrational by somewhat similar methods. It turns out that proof by contradiction can be a powerful tool in this endeavor, even for logarithms that are irrational.