Clay Kitchings :: Sum of a Series Problem, posed in class on April 18, 2007 :: EMAT 6600

S₁ = 1 + 2 + 3 + … + n

S₂ = 1² + 2² + 3² + 4² + … + n²

S₃ = 1³ + 2³ + 3³ + … + n³.

Problem: Show that S₃ = S₁².

First, in my judgment, it would be helpful to know some closed formulas for each of the three sums. The S₁ is fairly well-known and I have proven this multiple times. I will take the liberty to state that S₁ may also be written as .

Next, I sought out to find a closed formula for the sum of the first n square numbers. (It is worth noting that upon completing this problem, it is not necessary to find a closed formula for this sum.)

As a fan of using consecutive differences, I chose this method to locate the degree of polynomial involved (if indeed it is a polynomial) as well as the coefficients of each term.

I used Excel to quickly find some sums as well as some consecutive differences:

n	n^2	sum first n^2	Consecutive diffs 1	consec diffs 2	consec diffs 3
1	1	1
2	4	5	4 = 5 - 1
3	9	14	9	5 = 9 - 4
4	16	30	16	7	2 = 7 - 5
5	25	55	25	9	2
6	36	91	36	11	2
7	49	140	49	13	2
8	64	204	64	15	2
9	81	285	81	17	2
10	100	385	100	19	2

Since the third-order differences are constant, we can conclude that the sum of the first n square integers is cubic. We set up a system of equations to find the coefficients a, b, c, and d of .

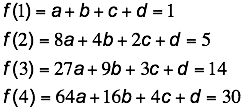
Solving the system yields a= 1/3, b = 1/2, c = 1/6, and d=0. I solved this by generating a 4x5 matrix on my TI-84 and using the matrix reduced-row echelon form.

Using the chart feature of Excel can also be helpful in helping individuals see the relationship once it is determined to be a polynomial of a particular degree. The following chart was created within Excel. (You can “add trendline” from the chart menu.)

Therefore, we have a “closed” form to express the sum of the first n square integers. If f(n) is the nth square integer, then .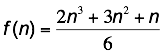

Let’s now investigate the next sum – the sum of the first n perfect cubes. I shall perform the operation the same way I did above using Excel. We obtain the following chart:

n	n^3	sum first n^3	consec diffs 1	consec diffs 2	consec diffs 3	consec diffs 4
1	1	1
2	8	9	8
3	27	36	27	19
4	64	100	64	37	18
5	125	225	125	61	24	6
6	216	441	216	91	30	6
7	343	784	343	127	36	6
8	512	1296	512	169	42	6
9	729	2025	729	217	48	6
10	1000	3025	1000	271	54	6

We observe that the fourth order differences are constant, thus implying a quartic polynomial. Setting up a system of equations as we did earlier (except with using five instead of four), we obtain the following:

If f(n) is the sum of the first n cubes, then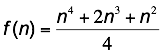

Now let’s try to verify that S₃ = S₁².

Let’s expand: 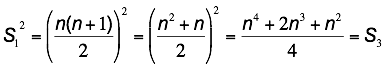(which is what we wanted to show.)