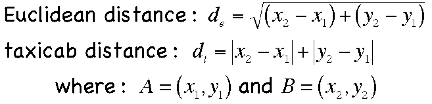TAXICAB GEOMETRY

by
Susan Sexton
Foundations of
Geometry I Project
University of
Georgia
Fall 2006
Instructor: Clint
McCrory
Distance in
Taxicab Geometry
Taxicab geometry is
very similar to Euclidean coordinate geometry.
The points, lines, angles
are all the same and measured in the same way.
What is different
is the notion of distance.
In Euclidean
coordinate geometry distance is thought of as “the way the crow flies”.
In taxicab geometry
distance is thought of as the path a taxicab would take.
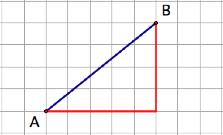
The blue path from
point A to B is the Euclidean distance from A to B.
The red path is the
taxicab distance from A to B.
While there is only
one Euclidean path from A to B, there are multiple taxicab paths from A to B.
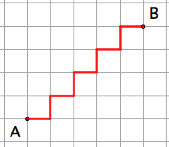
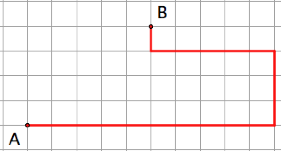
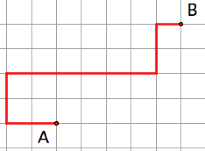
These are a few examples
of taxicab paths from A to B.
Which is the
shortest path?
Can you find an
even shorter path?
What do you think
would be the path a taxicab driver would take?
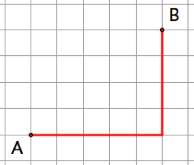
The taxicab
distance is defined as the sum of the
lengths of the vertical
and horizontal distances from A to B.
Mathematically, the
distance formulas for each geometry are: